Возвести число a в натуральную степень n – это значит найти произведение n одинаковых множителей, каждый из которых равен числу a, то есть

 

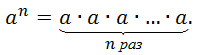
Возвести число a в целую отрицательную степень (–m) – это значит возвести число a в противоположную (положительную) степень m и найти обратную величину для полученного значения, то есть

 

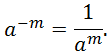
Любое действительное число a (a0) в степени нуль – это единица, то есть a⁰ = 1.

Рассмотрим равенство x⁴ = 16. Здесь x – это основание степени; 4 – показатель степени, 16 – степень. Основание степени x можно найти так: 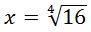 («икс равен корню степени четыре из числа 16» или «икс равен корню четвёртой степени из числа 16»). 

Корень степени n (n N, n 1) из действительного числа a – это действительное число b, n-я степень которого равна a, то есть

 

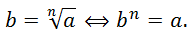
Нахождение корня степени n из числа a – это извлечение корня. Найти корень степени n из числа a – это значит извлечь корень. 

 (корень степени эн из числа а равен числу бэ) 

Извлечение корня – это действие. 

a – это подкоренное выражение, n – это показатель корня, b – это значение корня,     (радикал) – это знак корня.  

Возведение в степень и извлечение корня – это обратные действия. 

По определению корня  

Извлечь корень – это значит найти основание степени по степени и её показателю. 

Если aⁿ = b и a ? 0, b ? 0, n N (n 1), то число a – это арифметический корень степени n из числа b (арифметический корень энной степени из числа b). 

Возвести действительное число a в рациональную степень    – это значит извлечь корень степени n из числа a в степени m, то есть

 

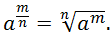
Замечание. Найти точное значение корня из действительного числа можно не всегда. Например, нельзя найти точное значение выражений: Значения таких выражений – это бесконечные непериодические десятичные дроби. То есть это иррациональные числа.