Сумму одинаковых слагаемых можно записать в виде произведения:
7 + 7 + 7 + 7 + 7 = 7 · 5, a + a + a + a+ a + a = a · 6. В этом случае запись становится короче. 

Произведение одинаковых множителей также можно записать короче:
2 · 2 · 2 · 2 · 2 · 2 = 2⁶, x · x · x · x = x⁴. Это степень. Читаем степени так: «два в степени шесть», «икс в степени четыре». 

Другими словами, произведение одинаковых множителей можно записать в виде степени. 

Например, запись 3⁴ – «три в степени четыре» – означает 3 · 3 · 3 · 3. Число 3 – это основание степени, число 4 – это показатель степени. Число 4 показывает, сколько раз нужно взять множителем основание – число 3. Таким образом, 3⁴ = 3 · 3 · 3 · 3 = 81. 

Таким образом, степень числа a с натуральным показателем n (n > 1) – это произведение n множителей, каждый из которых равен a. 

 

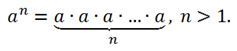
 – это возведение в степень 

(a в степени n равно числу b)

Возведение в степень – это действие. 

a и n – это компоненты действия возведения в степень, a – это основание степени, n – это показатель степени. 

b – это результат действия возведения в степень, b – это степень,  – это тоже степень.  

Любое число в степени один равно самому числу, то есть

3¹ = 3, 6¹ = 6, … , a¹ = a. 

Возвести число a в натуральную (целую положительную) степень n – это значит найти произведение n одинаковых множителей, каждый из которых равен числу a. 

Запомните!  

=	(Что?) возвести в степень (что?)	Десять возвести в степень четыре	104
	Возвести (что?) в степень (что?)	Возвести десять в степень четыре
	(Что?) возвести в (какую?) степень	Десять возвести в четвёртую степень
	Возвести (что?) в (какую?) степень	Возвести десять в четвёртую степень