Действие деления 1 : 2 для натуральных чисел выполнить нельзя. Чтобы найти частное 1 : 2, нужно расширить ряд целых неотрицательных чисел. Для этого запишем частное 1 : 2 как  («одна вторая»). Это обыкновенная дробь. Числа
(«одна вторая»). Это обыкновенная дробь. Числа 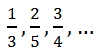 («одна третья, две пятых, три четвёртых») – это тоже обыкновенные дроби.
(«одна третья, две пятых, три четвёртых») – это тоже обыкновенные дроби. ![]()
Число, которое можно записать в виде  («пэ кутых»), где p, q
(«пэ кутых»), где p, q  N, – это положительная обыкновенная дробь (положительное дробное число).
N, – это положительная обыкновенная дробь (положительное дробное число). ![]()
Число p, которое стоит над чертой, – это числитель дроби. Число q, которое стоит под чертой, – это знаменатель дроби. Черта дроби – это знак деления числителя на знаменатель. ![]()
Знаменатель дроби показывает, на сколько частей мы разделили число один (единицу). Числитель дроби показывает, сколько частей мы взяли. Поэтому чтобы получить число
 из числа один, надо разделить число один на q равных частей и взять p таких частей.
из числа один, надо разделить число один на q равных частей и взять p таких частей. Любое натуральное число – это дробь, у которой знаменатель равен числу один:
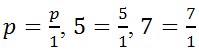 .
.
Если числитель дроби меньше, чем её знаменатель, то это – правильная дробь. Число
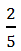 – это правильная дробь, так как числитель 2 меньше, чем знаменатель 5.
– это правильная дробь, так как числитель 2 меньше, чем знаменатель 5. Если числитель дроби больше или равен её знаменателю, то это – неправильная дробь. Число 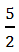 – это неправильная дробь, так как числитель 5 больше, чем знаменатель 2. Число
– это неправильная дробь, так как числитель 5 больше, чем знаменатель 2. Число
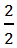 – это тоже неправильная дробь, так как числитель 2 равен знаменателю 2.
– это тоже неправильная дробь, так как числитель 2 равен знаменателю 2. Если числитель неправильной дроби не делится нацело на знаменатель, то неправильную дробь можно записать как сумму натурального числа и правильной дроби. ![]()
Например, 
![]()
Сумма натурального числа и правильной дроби – это смешанная дробь. Смешанная дробь имеет две части: 8 – это целая часть,  – это дробная часть.
– это дробная часть. ![]()
Смешанная дробь получена сложением натурального числа и правильной дроби. Натуральное число в смешанной дроби – это её целая часть, а правильная дробь – это дробная часть смешанной дроби. ![]()
Чтобы записать неправильную дробь как смешанную, надо её числитель разделить на знаменатель. ![]()
Если деление можно выполнить нацело, то неправильная дробь равна натуральному числу. ![]()
Например, 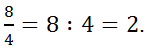
![]()
Если деление можно выполнить только с остатком, то неполное частное – это целая часть смешанной дроби, остаток – это числитель, а делитель – знаменатель дробной части. ![]()
Например, 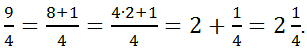
![]()
Чтобы записать смешанную дробь как неправильную, надо знаменатель дробной части умножить на целую часть и прибавить к числителю. Полученное число – это числитель новой дроби. Знаменатель нужно оставить без изменений. ![]()
Например, ![]() .
. ![]()
![]()
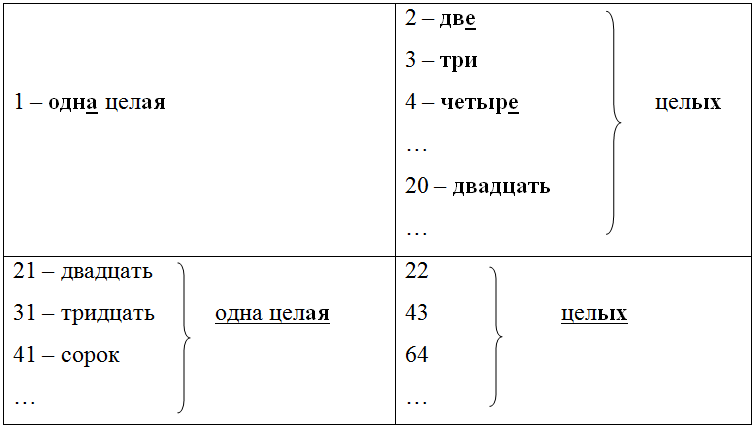
Запомните, как читать порядковые числительные! ![]()
|
|
Какой? |
Какая? |
Какое? (ср.р.) |
Какие? |
Каких? |
|
|
1 |
Первый |
Первая |
Первое |
Первые |
Первых |
|
|
2 |
Второй |
Вторая |
Второе |
Вторые |
Вторых |
|
|
3 |
Третий |
Третья |
Третье |
Третьи |
Третьих |
|
|
4 |
Четвёртый |
Четвёртая |
Четвёртое |
Четвёртые |
Четвёртых |
|
|
5 |
Пятый |
Пятая |
Пятое |
Пятые |
Пятых |
|
|
6 |
Шестой |
Шестая |
Шестое |
Шестые |
Шестых |
|
|
7 |
Седьмой |
Седьмая |
Седьмое |
Седьмые |
Седьмых |
|
|
8 |
Восьмой |
Восьмая |
Восьмое |
Восьмые |
Восьмых |
|
|
9 |
Девятый |
Девятая |
Девятое |
Девятые |
Девятых |
|
|
10 |
Десятый |
Десятая |
Десятое |
Десятые |
Десятых |
|
|
20 |
Двадцатый |
Двадцатая |
Двадцатое |
Двадцатые |
Двадцатых |
|
|
21 |
Двадцать первый |
Двадцать первая |
Двадцать |
Двадцать первые |
Двадцать первых |
|
|
30 |
Тридцатый |
Тридцатая |
Тридцатое |
Тридцатые |
Тридцатых |
|
|
40 |
Сороковой |
Сороковая |
Сороковое |
Сороковые |
Сороковых |
|
|
50 |
Пятидесятый |
Пятидесятая |
Пятидесятое |
Пятидесятые |
Пятидесятых |
|
|
52 |
Пятьдесят второй |
Пятьдесят вторая |
Пятьдесят второе |
Пятьдесят вторые |
Пятьдесят вторых |
|
|
60 |
Шестидесятый |
Шестидесятая |
Шестидесятое |
Шестидесятые |
Шестидесятых |
|
|
100 |
Сотый |
Сотая |
Сотое |
Сотые |
Сотых |
|
|
1000 |
Тысячный |
Тысячная |
Тысячное |
Тысячные |
Тысячных |
Запомните! ![]()

Запомните! ![]()
![]()
![]()