
Ри́ман, Гео́рг Фри́дрих Бе́рнхард
(нем. Georg Friedrich Bernhard Riemann)
Родился 17 сентября 1826 года — умер 20 июля 1866 года
Бернхард Риман — математик, механик, физик. Работая в области математики, внёс весомый вклад и усовершенствовал такие её разделы, как математический анализ, дифференциальная геометрия, математическая физика, арифметика и топология.
Риман родился в городе Брезеленц (Ганновер), рос в бедной семье, поэтому, несмотря на способности к математике, в школу смог поступить лишь в 14 лет. Далее своё обучение продолжил в Гёттингенском университете, где его учителем был Карл Фридрих Гаусс. Своё обучение Риман завершил защитой диссертации «Основания теории функций комплексной переменной», в которой впервые вводилось понятие, позже получившее название риманова поверхность (рис. 1). Далее занимался научной и преподавательской деятельностью.
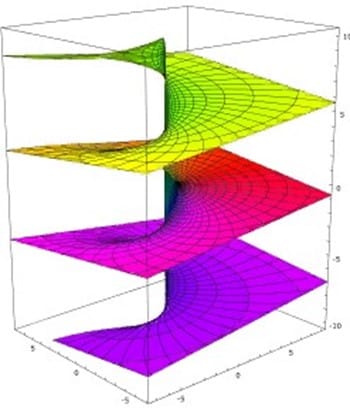
Риман в своей работе «О числе простых чисел, не превышающих заданной величины», исследовал простые числа и свойства ζ-функции[1]. После чего был избран членом Берлинской и Парижской академий наук, Лондонского королевского общества.
Большое количество понятий математики носят имя учёного: риманова метрика, риманова поверхность, риманова геометрия, интеграл Римана, гипотеза Римана и многие другие.
Гипотеза Римана.
ζ-функция Римана принимает нулевые значения только в отрицательных чётных числах 0 = ζ(−2) = ζ(−4) = … и комплексных числах с вещественной частью 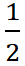 .
.
Риман является величайшим математиком XIX века, который преобразовал математику и внёс большой вклад в развитие различных её областей.
1 ζ-функции — дзета-функция Римана.

Тью́ринг, А́лан Мэ́тисон
(англ. Alan Mathison Turing)
Родился 23 июня 1912 года — умер 7 июля 1954 года
Выдающийся английский математик, логик, криптограф родился в Лондоне. Алан рос одарённым ребёнком. Но в школах, где он обучался, уделяли внимание гуманитарным наукам, а не математике, которой увлекался Тьюринг. С 1931 по 1934 год Алан Тьюринг учился в Королевском колледже Кембриджа.
В 1936 году Алан опубликовал работу, в которой описал положение об абстрактной вычислительной машине, получившей имя «машина Тьюринга». Машина Тьюринга — это математическая модель идеального вычислительного устройства (рис. 1). Идея машины Тьюринга — создание программы, которая хранится в памяти вычислительной машины и может решать любые задачи путём последовательного выполнения операций.
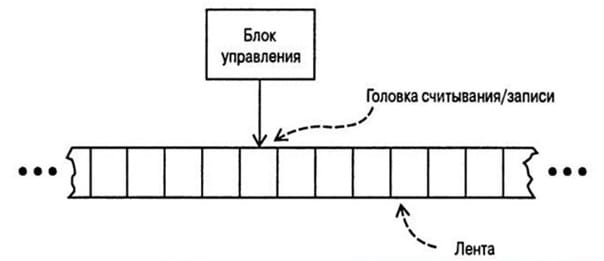
В 1938 году в Принстоне (США) Тьюринг защитил докторскую диссертацию на тему «Логические системы, основанные на ординалах».
Во время Второй мировой войны Алан Тьюринг занимался криптографией — разработал методы дешифровки кодов «Энигма», разработал и построил машину для автоматической расшифровки сообщений.
В 1946 году учёный разработал первый компьютер ACE, у которого была возможность хранения программ в памяти. А в 1950 году Тьюринг опубликовал тест под названием «Игра в имитацию». Смысл этого теста в том, что если человек, взаимодействующий с компьютером, не сможет отличить машину от человека, то можно считать, что компьютер умеет мыслить. Эта идея дала толчок к работам в области искусственного интеллекта и машинного обучения.
Также Алан Тьюринг создал и запрограммировал музыкальную машину — машину, которая могла воспроизводить музыкальные звуки, заложил основы для исследований в биологии с применением математических моделей, что нашло применение в технологии клонирования, биомедицинских исследованиях, создании новых лекарств.
Машина Тьюринга

Фале́с Миле́тский
(др.-греч. Θαλῆς ὁ Μιλήσιος)
Родился в период с 637 по 624 годы до нашей эры — умер в период с 558 с 547 годы до нашей эры
Древнегреческий философ и математик из Милета в Малой Азии. До настоящего времени дошли противоречивые данные о его происхождении, годах жизни. По разным данным, в том числе из легенд, известно, что Фалес много путешествовал, побывав в крупнейших городах Древнего Египта. Труды Фалеса не сохранились. Упоминания о его работах можно найти в трудах других древних учёных, которые жили после Фалеса.
Фалеса считают самым древним из известных великих математиков. Ему приписывают четыре математических открытия (из области геометрии).
- Диаметр делит круг на две равные части.
- В равнобедренном треугольнике углы при основании равны.
- Вертикальные углы, образованные при пересечении двух прямых, равны.
- Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны (второй признак равенства треугольников).
Опираясь на приведённые утверждения, Фалесом были сформулированы утверждения, которые в настоящее время носят его имя.
Теорема Фалеса о пропорциональных отрезках.
«Если на одной из двух прямых отложить последовательно несколько отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой пропорциональные отрезки» (рис. 1).
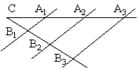
Обратная теорема Фалеса.
«Если прямые, пересекающие две другие прямые (параллельные или нет), отсекают на обеих из них равные (или пропорциональные) между собой отрезки, начиная от вершины, то такие прямые параллельны».
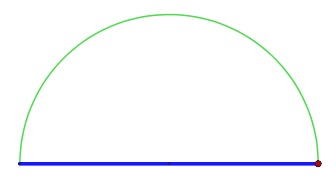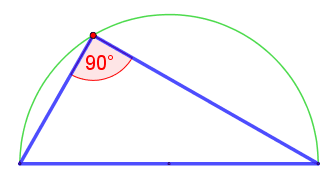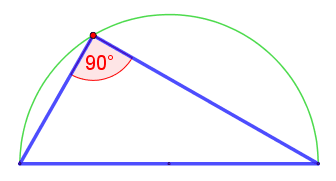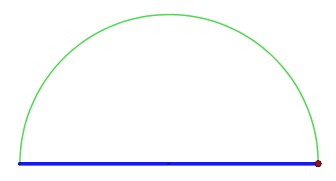
Но в немецких, англоязычных и некоторых других математических источниках имя Фалеса закреплено за другой теоремой: «Если в треугольнике угол опирается на диаметр окружности, описанной вокруг него, то этот угол — прямой, то есть треугольник — прямоугольный» (рис. 2).
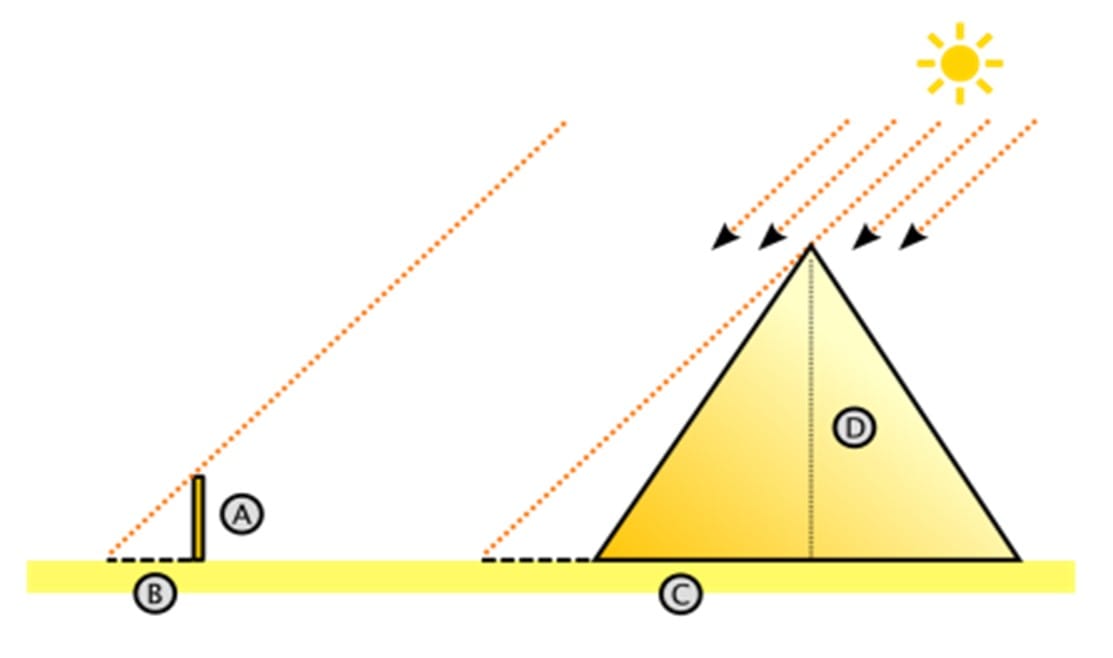
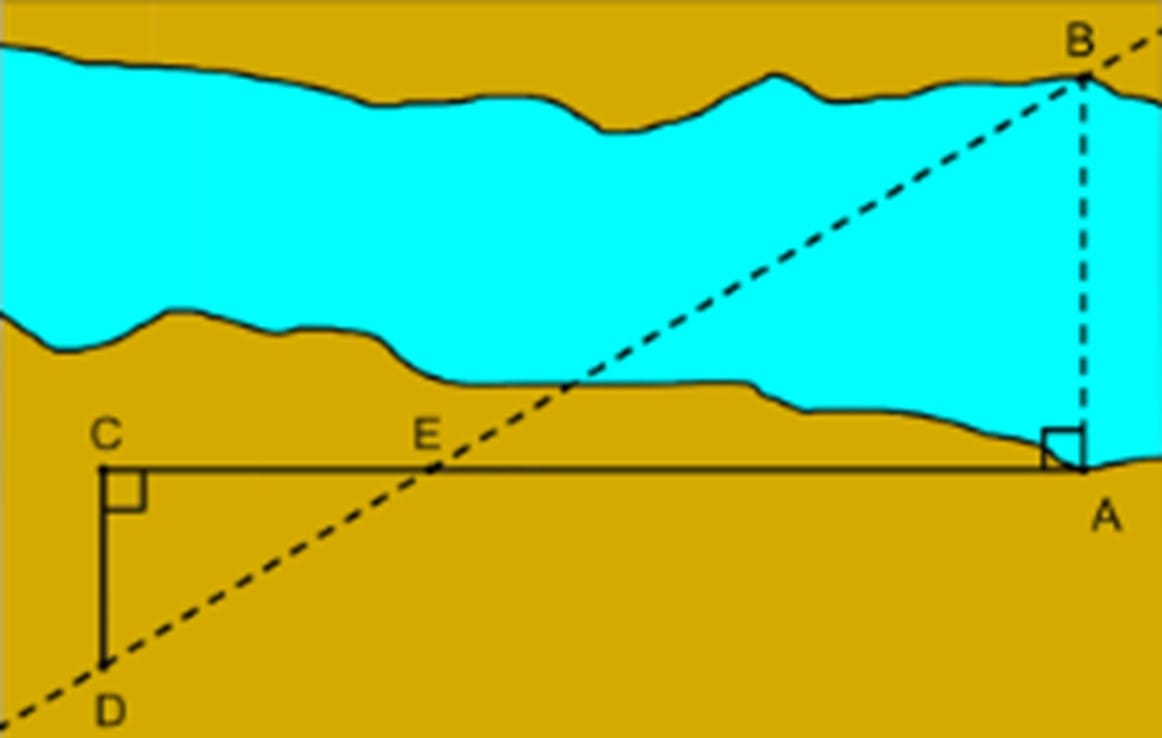
Утверждения, сформулированные Фалесом, использовались для разделения сегмента на несколько равных частей и позволяли измерить высоту пирамиды по её тени (рис. 3), расстояние до находящегося вдали корабля (рис. 4).

Ферма́, Пьер де
(фр. Pierre de Fermat)
Родился между 31 октября и 6 декабря 1607 года — умер 12 января 1665 года
Французский математик, который является одним из основоположников и создателей аналитической геометрии, математического анализа, теории вероятностей и теории чисел, родился в городе Бомон-де-Ломань, во Франции.
Пьер Ферма стал известным не только благодаря своему единственному труду «Трактат о спрямлении», но в большей степени своими переписками с другими учёными и заметками-пояснениями на полях в книге Диофанта[1], которые впоследствии опубликовал сын Пьера.
Разработка теории чисел является главной заслугой Ферма. В письмах со своими современниками он часто предлагал различные арифметические задачи, которыми интересовался сам. Например, найти общее правило решения ax2 + 1 = y2 в целых числах, при a = 149, 109, 433. Данная задача получила название «Второй вызов математикам».
Малая теорема Ферма.
Если p — простое число и a — целое число, не делящееся на p, то ap−1 − 1 делится на p.
Ферма разработал способ систематического нахождения всех делителей числа, но многие его методы решений остались неизвестными.
Ещё одна гипотеза Пьера Ферма: простые числа вида 4k + 1 представляются в виде суммы двух квадратов (5 = 4 + 1; 13 = 9 + 4), причём единственным способом, а для чисел, содержащих в своём разложении на простые множители простые числа вида 4k + 3 в нечётной степени, такое представление невозможно. Данное утверждение, как и некоторые другие задачи Пьера, впоследствии доказал немецкий математик Леонард Эйлер. Сам же Ферма свои математические умозаключения приводил практически всегда без доказательств (это было свойственно большинству математикам того времени).
Ферма интересовался изучением фигурных чисел (треугольные числа, квадратные числа и так далее). В связи с этим была сформулирована «Золотая теорема». Но самой известной теоремой знаменитого французского учёного является «Великая теорема Ферма».
Великая теорема Ферма.
Для любого натурального числа n > 2 уравнение an + bn = cn не имеет решений в целых ненулевых числах a, b, c.
Ферма был великим математиком, который заложил хороший фундамент для дальнейших исследований и открытий учёных, таких как Эйлер, Ньютон и других.
1 Диофант — древнегреческий математик, живший в III веке н. э.

Фибона́ччи, Леона́рдо Пиза́нский
(лат. Leonardus Pisanus, итал. Leonardo Pisano)
Родился приблизительно в 1170 году — умер приблизительно в 1250 году
Первый крупный математик средневековой Европы родился в Италии, в городе Пиза приблизительно в 1170 годe. Точная дата рождения неизвестна. Его отец был торговцев, много ездил. Чтобы дать образование сыну, он отправил его в Алжир, где Леонардо обучался у арабских учителей математике — искусству вычислений. Кроме Алжира, Фибоначчи обучался и в Египте, Сирии, Византии, Сицилии.
Свой первый и самый главный труд «Книгу абака» Фибоначчи начал писать в 1200 году. В этой книге Леонардо Фибоначчи максимально подробно и понятно описал все сведения из арифметики и алгебры, которые были известны к тому времени, на основе десятичной системы счисления (индийского счёта) — действия с целыми числами, обыкновенными дробями, решение задач на пропорции, смешение, суммирование прогрессий (арифметической и геометрической), возвратного ряда, извлечение квадратного и кубического корней. В этой работе Леонардо Пизанский впервые использовал отрицательные числа.
Вторая работа Фибоначчи «Практика геометрии» посвящена доказательствам теорем, связанных с измерительными методами. Кроме описания уже известных фактов, Леонардо приводит и свои — доказательство того, что три медианы треугольника пересекаются в одной точке, определение числа π с помощью вписанного и описанного 96-угольника.
В работе «Цветок» Фибоначчи провел исследование кубического уравнения 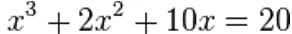 и показал, что его корень будет иррациональным.
и показал, что его корень будет иррациональным.
Труд «Книга квадратов» включает в себя задачи на решение неопределённых квадратных уравнений. Также в этой работе Фибоначчи показал, что числа x2 + y2 и x2 − y2 не могут быть одновременно квадратными[1].
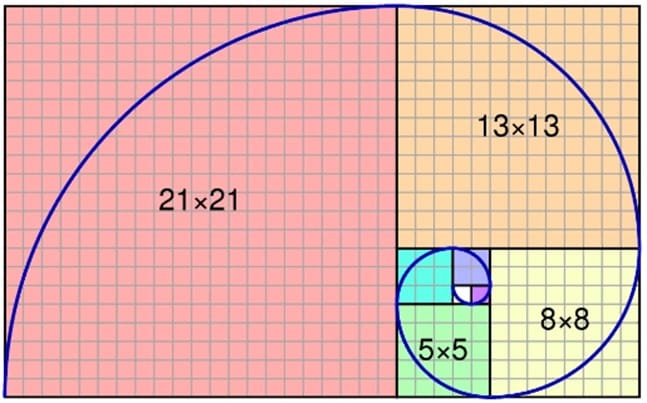
Наибольшую известность учёному принесла задача, описывающая рост популяции кроликов. Последовательность чисел, в которой каждый следующий элемент — это сумма двух предыдущих, в последствии была названа числами Фибоначчи (рис. 1):
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229, 832040, …
1 Квадратное число (идеальный квадрат) — это число, которое является точным квадратом целого числа.

Фурье́, Жан-Бати́ст
(фр. Jean-Baptiste Joseph Fourier)
Родился 21 марта 1768 года — умер 16 мая 1830 года
Жан-Батист Фурье — французский математик и физик. Фурье был членом различных академий наук, в том числе и Петербургской, был членом Лондонского королевского общества.
Фурье хорошо учился, показывая успехи в латинском и французском языках, риторике, математике, механике и пении. Но особенно он был увлечён математикой. Так, в возрасте 14 лет освоил шеститомный труд Безу[1] «Курс математики». Позже стал преподавателем, вёл научную работу.
Фурье начал свою исследовательскую деятельность, представив работу о численном решении уравнений любой степени. Он изложил теорему, названную в будущем его именем, о числе действительных корней алгебраического уравнения, лежащих между данными границами.
Работая над распространением тепла в твёрдом теле, Фурье представил разложение функций в тригонометрические ряды (ряды Фурье). Эта работа подверглась критике со стороны его современников. Но позднее была признана и получила Большую премию Французской академии. В теории распространения тепла Фурье использовал свои методы — ряды Фурье и интеграл Фурье. Данное исследование описано в монографии «Аналитическая теория тепла». Вскоре ряды Фурье и интеграл Фурье стали широко использоваться другими математиками в решении широкого круга различных задач.
Ряд Фурье — это представление периодической функции в виде ряда
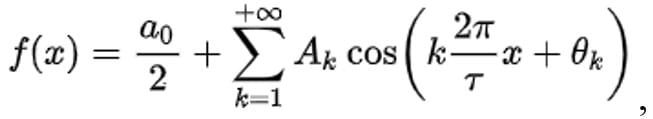
где Ak — амплитуда k-го гармонического колебания;
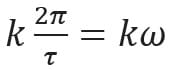 — круговая частота гармонического колебания;
— круговая частота гармонического колебания;
θk — начальная фаза k-го колебания.
Имя Фурье внесено в список величайших учёных Франции, который размещён на первом этаже Эйфелевой башни.
1 Этьен Безу — французский математик (1730 — 1783).

Хайя́м, Ома́р (عمر خیام)
Гия́с-ад-Ди́н Абу-ль-Фатх Ома́р ибн Ибрахи́м Хайя́м Нишапури́
(перс. غیاث الدین ابوالفتح عمر بن ابراهیم خیام نیشابورﻯ)
Родился 18 мая 1048 года — умер 4 декабря 1131 года
Персидский философ, математик, астроном и поэт родился в Иране, в городе Нишапур. С раннего детства проявлял интерес к различным наукам, особенно к математике, астрономии и философии. Известен как поэт и философ, математик и астроном. В Иране, Таджикистане и Афганистане считается национальным поэтом. Автор цикла философских четверостиший (рубаи). Обучался в медресе в Нишапуре, Самарканде, Бухаре, Балхе.
Омар Хайям, используя труды Аристотеля, Евклида и других учёных, внёс большой вклад в развитие арифметики, алгебры и геометрии. Его работы в математике можно разделить по направлениям — теория отношений, теория параллельных, учение о числе.
В своём сочинении «Трактат о доказательствах проблем ал-джебры и ал-мукабалы» Омар Хайям описал типы и методы решения линейных, квадратных и кубических уравнений, обосновал геометрический метод Архимеда, дал оценку количества положительных корней уравнений и их величины, указал алгоритм выбора типа канонического сечения. Только Хайям не заметил, что кубическое уравнение может иметь три положительных вещественных корня. Также в этой работе дал первое дошедшее до нас определение алгебры как науки об определении неизвестных величин, которые состоят в отношениях с известными величинами, и такое определение осуществляется с помощью составления и решения уравнений.
В работе «Комментарии к трудностям во введениях книги Евклида» Омар Хайям предпринял попытку доказать пятый постулат Евклида[1], опираясь на следующее утверждение: «Две сходящиеся прямые пересекаются, и невозможно, чтобы прямые расходились в направлении схождения». Также в этой работе автор доработал теорию отношений и пропорций и учение о числе — иррациональные числа учёный рассматривал наравне с рациональными.
Методу извлечения корней любой степени из целых чисел, в основе которого лежала формула, в настоящее время известная как бином Ньютона, посвящена работа «Трудности в математике». А в труде «Вес мудрости» Омар Хайям описал два решения известной задачи Архимеда об определении количества золота и серебра в сплаве.
Омар Хайям в математику привнёс много нового, классифицировал уравнения, выдвинул теорию геометрических решений алгебраических уравнений. Дойти до явных алгебраических формул Хайаму не удалось, но, несмотря на это, он заложил для них хороший фундамент.
1 Пятый постулат Евклида: если на плоскости при пересечении двух прямых третьей сумма односторонних внутренних углов меньше 180°, то эти прямые при продолжении рано или поздно пересекутся с той стороны, с которой эта величина (сумма) меньше 180°.
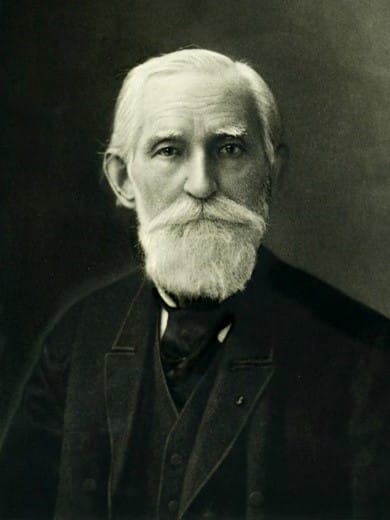
Чебышёв, Пафну́тий Льво́вич
Родился 16 мая 1821 года — умер 8 декабря 1894 года
Русский математик, механик, основоположник петербургской математической школы родился в Калужской губернии в дворянской семье. Образование получал домашнее. В 1832 году семья переехала в Москву, где с 1837 года Чебышёв начал изучение математики в Московском университете. В 1841 году Пафнутий окончил университет, а в 1846 году успешно защитил магистерскую диссертацию «Опыт элементарного анализа теории вероятностей», которая была напечатана как учебное пособие.
Чтобы получить право чтения лекций в Петербургском университете, Чебышёв защитил ещё одну диссертацию — «Об интегрировании с помощью логарифмов». В дальнейшем, в 1849 году он защитил докторскую диссертацию «Теория сравнений» и через год стал профессором Петербургского университета.
П. Л. Чебышёв проводил исследования в таких областях математики, как
— теория чисел. Получил лучшее, чем известное в то время, приближение функции распределения простых чисел — интегральный логарифм 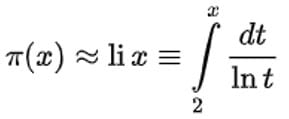 , занимался исследованием проблем делимости натуральных чисел и их разложения на простые множители;
, занимался исследованием проблем делимости натуральных чисел и их разложения на простые множители;
— теория вероятностей. Пафнутий Львович был первым, кто ввёл случайные величины[1] как основное понятие теории вероятностей (рис. 1). Теорема Чебышёва о том, что среднее арифметическое случайных величин при достаточно большом n сколь угодно мало (по вероятности) отклоняется от постоянной величины, легла в основу современной теории вероятностей. А доказанное им неравенство 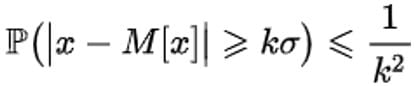 , которое носит его имя, Чебышёв применил для обоснования закона больших чисел[2]. Работы по усовершенствованию дальнобойности и точности артиллерийской стрельбы использовались для апробации методов теории вероятностей.
, которое носит его имя, Чебышёв применил для обоснования закона больших чисел[2]. Работы по усовершенствованию дальнобойности и точности артиллерийской стрельбы использовались для апробации методов теории вероятностей.
Также известны труды Пафнутия Львовича по теории приближения функций, математическому анализу, геометрии, прикладной математике и его механизмы. Так, Чебышёв сконструировал два варианта арифмометра. На первом (рис. 1) можно было только складывать и вычитать, а второй (рис. 2) уже имел множительную приставку.


1 Случайная величина — это переменная, значения которой — численные исходы некоторого случайного эксперимента.
2 Закон больших чисел — принцип, который описывает результат выполнения одного и того же эксперимента много раз.

Э́йлер, Леона́рд
(нем. Leonhard Euler)
Родился 15 апреля 1707 года — умер 18 сентября 1783 года
Леонард Эйлер является гениальным учёным, занимавшимся исследовательской деятельностью в различных научных областях: математика, физика, астрономия, кораблестроение, теория музыки и др. Изучал химию, ботанику, медицину и другие науки, был полиглотом. Родился в городе Базель (Швейцария).
Эйлер является автором большого количества трудов (около 850), включая статьи и монографии по математическому анализу, дифференциальной геометрии, теории чисел, приближённым вычислениям, небесной механике, математической физике и другим.
Эйлер упорядочил и связал в общую систему алгебру, геометрию, тригонометрию и другие математические дисциплины. Символика современной школы математики практически неизменна со времён Эйлера.
Стоит выделить из математических открытий Леонардо следующие: формула Эйлера, сравнение по целому модулю, полная теория непрерывных дробей, многочисленные приёмы интегрирования и решения дифференциальных уравнений, число Эйлера e [1], обозначение i для мнимой единицы[2].
Формула Эйлера.
Для любого вещественного числа x выполнено следующее равенство: 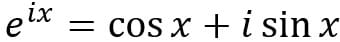 , где e — математическая константа, которая определяется по формуле
, где e — математическая константа, которая определяется по формуле 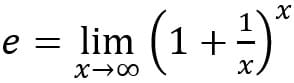 , i — мнимая единица.
, i — мнимая единица.
Сравнение по модулю.
Если два целых числа a и b при делении на m дают одинаковые остатки, то они называются сравнимыми по модулю числа m.
Например, числа 32 и −10 сравнимы по модулю 7, так как оба числа при делении на 7 дают остаток 4: 32 = 7 ⋅ 4 + 4; −10 = 7 ⋅ (−2) + 4.
Также числа 32 и —10 сравнимы по модулю 7, так как их разность 32 minus; (−10) = 42 делится на 7 и к тому же имеет место представление 32 = 6 ⋅ 7 + (−10).
В теории чисел Эйлер доказал или опроверг множество гипотез, предложенных другими учёными, решил задачи, которые не были решены более 70 лет, со времён Ферма.
Так, например, Леонардо Эйлер доказал, что число 231 − 1 простое число; доказал утверждение, что все числа вида Fn = 22n + 1 не являются простыми, оказалось, что при n = 5 число делится на 641.
Эйлер доказал «Великую теорему Ферма» для n = 3 и n = 4.
В математическом анализе Эйлер в монографиях «Введение в анализ бесконечно малых», «Дифференциальное исчисление» и «Интегральное исчисление» разработал курс, в котором описывается символика, приведены примеры, разработаны методика и технические приёмы, которые используются в настоящее время в классическом анализе. Эйлер первый ввёл двойные интегралы. Современное определение показательной, логарифмической и тригонометрических функций — тоже его заслуга, как и их символика и обобщение на комплексный случай.
Эйлер внёс огромный вклад в теорию чисел, алгебру, математический анализ, геометрию, комбинаторику, теорию графов, теоретическую механику. Эйлер заложил фундамент, преобразовал и усовершенствовал почти все области математики и связанные с ней науки.
Умер в Санкт-Петербурге (Российская Империя).
1 Число e — основание натурального логарифма, математическая константа, иррациональное число. Приближённо равно 2,71828… .
2 Мнимая единица i — число, такое, что i2 = −1.

Яко́би, Карл Гу́став Я́коб
(нем. Carl Gustav Jacob Jacobi)
Родился 10 декабря в 1804 года — умер 18 февраля 1851 года
Якоби — немецкий математик и механик. Преобразовал различные разделы математики: комплексный анализ, линейную алгебру и другие. Карл Густав являлся членом Берлинской, Парижской, Петербургской академий наук, иностранным членом Лондонского королевского общества.
Карл родился в пригороде Берлина, в Потсдаме, в семье банкира.
Якоби после окончания гимназии поступил в Берлинский университет, проявлял себя способным студентом. По завершении обучения защитил диссертацию, посвящённую разложению рациональных функций на простейшие дроби. В педагогической работе показал себя талантливым преподавателем.
Первые исследования Якоби были в области теории эллиптических функций, считается основателем этого раздела математики. Данные исследования описаны Карлом Густавом в труде «Новые основания эллиптических функций», здесь он разработал теорию тета-функций Якоби.
Якоби занимался вариационным исчислением (исследовал вторую вариацию и получил достаточные условия экстремума). В теории чисел составил таблицу индексов для всех простых чисел до 1000. Якоби открыл функциональные определители, которые позже стали называться якобианами.
Якоби доказал утверждение Ферма, что каждое натуральное число можно представить в виде суммы не более 4 квадратов, при этом нашёл число способов такого представления.
Якоби ввёл в общее употребление символ «∂» для обозначения частной производной.
В математике много терминов и понятий, к открытию и исследованию которых Карл Густав имеет непосредственное отношение, носят имя учёного: матрица Якоби (рис. 1), символ Якоби, тождество Якоби и другие.
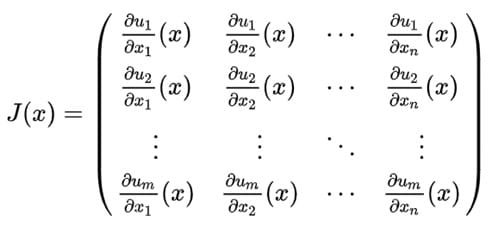
Якоби — учёный, который совершил много открытий в математике, усовершенствовал различные её области.