
Лагранж Ж. 
Лаплас П. 
Лейбниц Г. 
Лобачевский Н. 
Мандельброт Б. 
Нейман Дж. 
Ньютон И. 
Нэш Дж. 
Остроградский М. 
Паскаль Б. 
Пифагор 
Пуанкаре А.

Лагра́нж, Жозе́ф Луи́
(фр. Joseph Louis Lagrange, итал. Giuseppe Lodovico Lagrangia)
Родился 25 января 1736 года — умер 10 апреля 1813 года
Французский учёный, математик, астроном, механик родился в Турине (Италия) в семье военного казначея. Своё обучение Жозеф Луи начал в Туринском колледже, где он должен был получить юридическое образование. Но работа Галилея «О преимуществах аналитического метода» настолько заинтересовала и увлекла, что Лагранж оставил юридические науки и погрузился в математику.
Вклад Лагранжа в систематизацию и развитие математики сложно переоценить. Его вместе с Леонардом Эйлером считают величайшими математиками XVIII века.
В 1755 году Жозеф Луи Лагранж отправил Эйлеру работу об изопериметрических свойствах, в которой решил несколько задач, решение которых Эйлер ещё не нашёл. Эта работа позже легла в основу вариационного исчисления. А в 1762 году Лагранж опубликовал первое описание общего решения вариационной задачи, позднее обоснованное Эйлером.
В 1766 году Лагранж переезжает в Берлин. Годы с 1766 по 1787 считаются самыми плодотворными в жизни учёного. За это время он опубликовал много важных работ.
Одним из направлений была алгебра и теория чисел. Жозеф Луи доказал некоторые утверждения Пьера Ферма, теорему Вильсона,[1].
В 1771 году Лагранж опубликовал работу «Размышления о решении числовых уравнений», в которой ввёл понятие «конечная группа подстановок», предположил, что не все уравнения выше четвёртой степени разрешимы в радикалах. Этот труд позднее получил своё развитие в работах Нильса Абеля и Эвариста Галуа.
Главной работой великого учёного стала «Аналитическая механика» (1788 год). В ней, помимо решения задач статики и динамики, автор ввёл обобщённые координаты, описал принцип наименьшего действия.
После возвращения в Париж учёный занимается решением задачи приближения функции многочленом и выводит формулу интерполяционного полинома,[2], названного в его честь.
В работе «Теория аналитических функций» Лагранж не пользуется бесконечно малыми, приводит формулу остаточного члена ряда Тейлора, метод множителей для решения задач на условный экстремум,[3], названные позднее его именем, и многое другое.
Кроме того, Лагранж получил две премии за работы в области астрономии.
1 Теорема Вильсона: для любого простого числа выражение делится на p.
2 Интерполяционный полином Лагранжа— многочлен минимальной степени, принимающий заданные значения в заданном наборе точек, то есть решающий задачу интерполяции.
3 Метод множителей Лагранжа— метод нахождения условного экстремума функции f(x), где x ∈ Rn, относительно m ограничений φi(x) = 0, где меняется от 1 до m.

Лапла́с, Пьер-Симо́н, маркиз
(нем. Peter Simon Pállas)
Родился 23 марта 1749 года — умер 5 марта 1827 года
Французский математик, физик, астроном родился в Нормандии. Работал в области дифференциальных уравнений, теории вероятностей, теории определителей, математической физики и других, в астрономии применял математические методы расчётов.
Пьер-Симон Лаплас получил образование в университете Кан. Лаплас выходец из крестьянской семьи, что в дальнейшем в революционные годы способствовало развитию его карьеры и позволяло занимать высокие должности.
Решая прикладные задачи, Лаплас разработал методы, которые использовались в дальнейших исследованиях многими учёными. Важные исследования Лапласа относятся к линейной алгебре, он разложил определители по минорам. Он обобщил и продвинул теорию вероятностей, применив её к дискретным случайным величинам. Ввёл производящие функции. Доказал в 1812 году одну из предельных теорем теории вероятностей — теорему Муавра—Лапласа. Так же Пьер-Симон Лаплас добился важных результатов в теории ошибок, теории приближений, теории потенциала и специальных функций. Его именем названо преобразование Лапласа (интегральное преобразование, связывающее функции комплексного и действительного переменного) и уравнение Лапласа — дифференциальное уравнение в частных производных
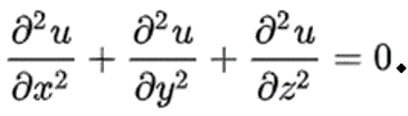
В разные годы Лаплас принимал участие в руководстве работами по созданию метрической системы. Основную единицу длины по предложению учёного назвали метром.
Лаплас своими исследованиями и открытиями привнёс в математическую науку много нового, усовершенствовал и обобщил её.

Ле́йбниц, Го́тфрид Вильге́льм
(нем. Gottfried Wilhelm von Leibniz)
Родился 1 июля 1646 года — умер 14 ноября 1716 года
Готфрид Вильгельм Лейбниц был немецким философом, логиком, математиком, механиком, физиком, юристом, историком, дипломатом, изобретателем и языковедом, прожившим всю свою жизнь в Священной Римской Империи.
В математике Лейбниц предложил несколько приёмов решения задач на нахождение касательных, экстремумов, квадратур, причём он провёл решение в обобщённом виде и распространил решение для дробных, иррациональных и трансцендентных функций,[1].
Большой вклад Лейбниц внёс в дифференциальное и интегральное исчисление (основанное на бесконечно малых — это функции предел которых равен нулю), в этой сфере его главный труд «Новый метод максимумов и минимумов».
В 1686 году Готфрид ввёл символ ∫(интеграл) и назвал интегрирование обратным действием к дифференцированию. Рассматривая решение линейных систем уравнений, Лейбниц практически ввёл понятие определителя. Он вывел первый ряд для числа π:
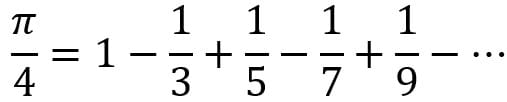
Так же он разложил рациональные дроби на сумму простейших, ввёл показательную функцию в общем виде uv.
Такие термины как «дифференциал», «дифференциальное исчисление», «дифференциальное уравнение», «функция», «переменная», «постоянная», «координаты», «абсцисса», «алгебраические и трансцендентные кривые», «алгоритм» были введены Лейбницем, причём очень приближённо к современным.
Готфрид Лейбниц описал в своих работах двоичную систему счисления с нулём и единицей. Можно сказать, что он стал первым программистом-теоретиком. Описанный им код навёл на мысль, что существуют совершенно другие законы математики, которые можно распространить на систему механики. Такая машина работала бы, по его мнению, на основе двоичного кода. Образ такой машины Лейбниц описал в труде в 1679 году (в реальности создать такую машину было тогда нереально из-за технических возможностей того времени).
В математике Лейбниц был не только теоретиком, но и практическим изобретателем. Его модель арифмометра,[2] (1673 год) могла вычислять не только сложение и вычитание, но и выполнять такие сложные операции, как умножение, деление, извлечение квадратных и кубических корней (рис. 1).


Лейбниц — математик, заложивший основу дифференциального и интегрального исчисления, выдвинул прогрессивные идеи в математической логике, заложил основу теории рядов и другое. Открытия Лейбница в математической науке сыграли важную роль в её становлении.
1 Нобелевская премия — наиболее престижная международная премия в области науки, литературы и общественной деятельности.
2 Арифмометр — вычислительная машина, предназначенная для выполнения арифметических действий. Прародитель современного калькулятора.

Лобаче́вский, Никола́й Ива́нович
Родился 1 декабря 1792 года — умер 24 февраля 1856 года
Великий русский математик, один из первооткрывателей неевклидовой геометрии родился в Нижнем Новгороде в семье чиновника. После смерти отца Николай с матерью и двумя братьями переехал в Казань. С этим городом связаны его образование, становление как учёного, педагога, руководителя.
С 1807 года Лобачевский обучался в недавно открытом Казанском университете у Мартина Бартельса, превосходного педагога из Германии, учеником которого был Карл Фридрих Гаусс. А в 1811 году Николай Лобачевский, успешно окончив университет со степенью магистра по физике и математике, остался в университете и с 1814 года получил курсы по теории чисел по Гауссу и Лежандру, курсы геометрии и тригонометрии. С 1820 по 1827 год Н. И. Лобачевский занимал должность декана физико-математического университета. А в 1827 году Николай Лобачевский был избран ректором Казанского университета. За этот период Лобачевский внёс неоценимый вклад в развитие университета.
Не оставлял он и науку. Главным делом своей жизни учёный видел развитие неевклидой геометрии. 23 февраля 1826 года — выступление с докладом «Сжатое изложение начал геометрии» — считается днём рождения неевклидовой геометрии.
Лобачевский, пытаясь доказывать пятый постулат Евклида о том, что «через точку, не лежащую на данной прямой, можно провести прямую, параллельную данной, и притом только одну», пришёл к противоположному утверждению — «Через точку, не лежащую на данной прямой, могут проходить две и более прямых, параллельных данной» (рис. 1). Это стало отправной точкой развития нового направления — геометрии Лобачевского.
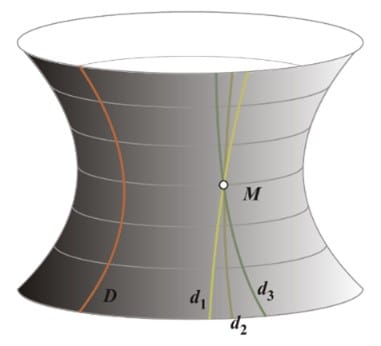
Геометрия Лобачевского описывает гиперболическое пространство, в котором «нарушались» многие законы евклидовой геометрии. Например, сумма углов в треугольнике в другой геометрии всегда меньше 180° (рис. 2).
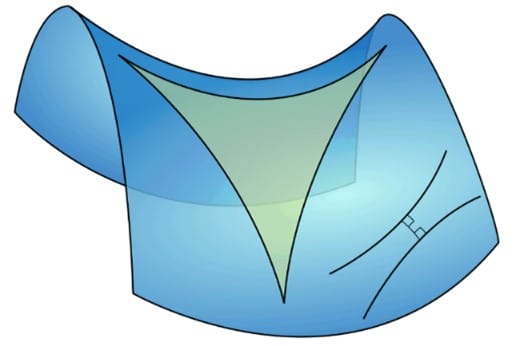
При жизни Лобачевский не получил признания. Его труды были резко раскритикованы известными учёными того времени, в частности, Михаилом Васильевичем Остроградским. Но он был не единственным в своей работе. Примерно в это же время Карл Фридрих Гаусс и Янош Боляй сделали такие же открытия.
По-настоящему открытие Лобачевского было оценено только в XX веке. Его геометрия привела к новым открытиям, например к теории относительности Альберта Энштейна.
Великие имена России. Николай Лобачевский
Геометрия Лобачевского

Мандельбро́т, Бенуа́
(фр. Benoît B. Mandelbrot)
Родился 20 ноября 1924 года — умер 14 октября 2010 года
Французский и американский математик, создатель фрактальной геометрии, родился в Варшаве (Польша). В 1936 году Мандельброты переехала в Париж (Франция), а во время Второй мировой войны семья жила на юге Франции. Необычайный математический дар — великолепное пространственное воображение — позволило окончить Политехническую школу Парижа и Сорбонну. После окончания Калифорнийского технологического университета (США) Мандельброт вернулся в Париж, где в 1952 году получил докторскую степень.
В 1958 году Бенуа Мандельброт с семьёй переехал в США и стал работать в научно-исследовательском центре IBM в Йорктауне. Там учёный занимался изучением возможности предсказания шумовых помех в электронных схемах при передаче данных на расстояние. Для решения данной задачи Бенуа впервые применил рекурсивный[1] метод построения специальных множеств, названных им фрактальными множествами.
Бенуа Мандельброт является отцом-основателем фрактальной геометрии.
Чтобы построить фрактальное множество, необходимо проделать огромное количество вычислений. С появлением мощной вычислительной техники у учёных такая возможность появилась. Мандельброт — первый, кто использовал компьютер для расчёта классического фрактала (рис. 1). Изначально изображение было чёрно-белым, позднее его раскрасили (рис. 2)


Одна из основных идей фрактальной геометрии — сложные геометрические фигуры обладают свойством самоподобия (рис. 3). Теория фракталов применяется в математических моделях экономики, физики, химии, астрономии, биологии, в компьютерной графике (построение изображений природных объектов).

Фрактал Мандельброта
Документальное кино памяти математика Бенуа Мандельброта.
Совершенная форма. Наука о фракталах
1 Рекурсивная последовательность — это последовательность, в которой каждый следующий элемент функционально зависит от предыдущих элементов.

Не́йман, Джон фон
(англ. John von Neumann)
Не́йман, Я́нош Ла́йош
(венг. Neumann János)
Родился 28 декабря 1903 года — умер 8 февраля 1957 года
Венгро-американский учёный, математик, физик, родился в Будапеште в семье адвоката, доктора юриспруденции. Янош был очень одарённым и разносторонне развитым мальчиком. Родители поддерживали Яноша во всех его начинаниях.
По окончании гимназии Нейман учился сразу по двум направлениям — в Католическом университете Петера Пазманя в Будапеште, окончив который в 23 года получил докторскую степень по математике и в Швейцарской технической школе Цюриха, где изучал химическую инженерию.
В 1926 году фон Нейман получил должность приват-доцента Берлинского университета имени Гумбольдта. В этот период Янош строит собственную аксиоматическую систему теории множеств, опубликовав её в работе «Аксиоматизация теории множеств».
Следующим направлением работы Неймана стала квантовая механика, для которой он установил строгую математическую основу, в настоящее время носящую имя аксиомы Дирака — фон Неймана.
На основе работ по построению математической теории квантовой механики Нейман перешёл к другому направлению — теории операторов, заложив основы современного функционального анализа.
Следующее направление работ Джона фон Неймана связано с прикладной математикой. Доказав теорему о минимаксе[1], Нейман фактически создал условия для возникновения нового раздела — теории игр.
С 1930 года Джон фон Нейман по приглашению переехал в США преподавать в университете Принстона. В этот период он знакомится с работой Алана Тьюринга об универсальных вычислительных машинах.
С 1945 по 1951 годы фон Нейман участвовал в проекте по созданию первого в мире лампового компьютера ЭНИАК и более совершенной машины EDVAC. В 1946 году учёный опубликовал «Предварительный доклад о машине EDVAC», в котором подробно описал как саму машину, так и её логические свойства. Его главная идея заключалась в том, что данные, с которыми работает программа, и сама программа должны находиться в оперативной памяти компьютера. Этот подход в настоящее время носит название «Архитектура фон Неймана» (рис. 1) и реализуется в большинстве современных компьютеров. Кроме того, Джон фон Нейман дал толчок развитию линейного программирования.
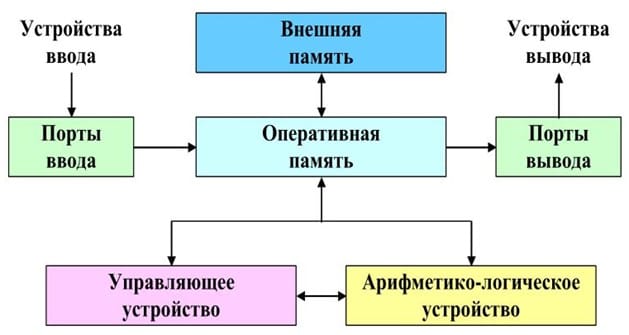
Базовые принципы архитектуры фон Неймана
1 Теорема о минимаксе: для любой конечной игры (двух игроков) с нулевой суммой существует «устойчивая» пара стратегий, для которых один проиграет, но с минимальным выигрышем, а другой игрок, при этом получит максимальный выигрыш, не прибегая к рискованной стратегии.

Нью́то́н, Исаа́к, сэр
(англ. Isaac Newton)
Родился 4 января 1643 года — умер 31 марта 1727 года
Величайший английский математик, физик, механик и астроном, один из создателей классической физики и математического анализа родился в деревне Вулсторп (графство Линкольншир, Англия) в семье фермера. В 1655 году Исаака отдали в школу, где он показал себя способным учеником. Дальнейшее образование Ньютон получил в колледже Святой Троицы Кембриджского университета.
Уже обучаясь в колледже, Исаак Ньютон совершил первые открытия в математике. К ним относятся: классификация кривых третьего порядка[1] (продолжение исследований Пьера Ферма кривых второго порядка) и биномиальное[2] разложение произвольной степени.

Для быстрого вычисления биномиальных коэффициентов можно использовать треугольник Паскаля. В случае нецелого значения n разложение представляет собой бесконечный ряд.
Причём последнее — это начало нового инструмента математического анализа — теория бесконечных рядов Ньютона. Сам Ньютон использовал ряды для решения уравнений, исследования поведения функций.
Следующим важнейшим открытием Ньютона стала разработка дифференциального и интегрального исчисления (почти одновременно с Готфридом Вильгельмом Лейбницем и независимо от него). Первое изложение своего варианта анализа Ньютон опубликовал только в 1693 году, спустя почти 30 лет с момента открытия. В современной науке используются ньютоновское обозначение О бесконечно малой dt и точка над буквой 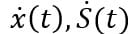 — производная по времени.
— производная по времени.
В 1704 году был опубликован труд «О квадратуре кривых», в котором Ньютон использует производные высших порядков, находит значения интегралов рациональных и иррациональных функций, приводит примеры решения дифференциальных уравнений первого порядка.
В других работах — «Универсальная арифметика» (1707 год), «Анализ с помощью уравнений с бесконечным числом членов» (1711 год), «Метод флюксий[3] и бесконечных рядов» (1736 год) — Исаак Ньютон приводит различные численные методы приближённого решения уравнений, исследования различных кривых, частные производные, разностную интерполяционную формулу (аналог формулы Тейлора), задачи нахождения экстремумов, касательных, нормалей, точек перегиба, радиусов и центров кривизны кривой и многое другое.
Наравне с биномом Ньютона широко известна и формула Ньютона—Лейбница нахождения значения определённого интеграла (рис. 1):
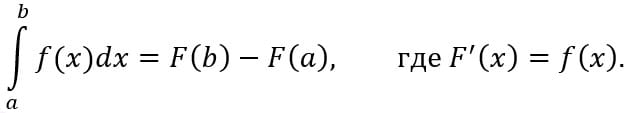
1 Плоская алгебраическая кривая третьего порядка — множество точек плоскости, заданных кубическим уравнением F(x, y, z) = 0.
2 Бином (двучлен) — полином, который состоит из двух слагаемых (a + b).
3 Флюксия — то же, что и производная, чаще всего, по времени.

Нэш, Джон Форбс, младший
(англ. John Forbes Nash, Jr.)
Родился 13 июня 1928 года — умер 23 мая 2015 года
Американский математик, исследователь теории игр, дифференциальной геометрии родился в городе Блудфил, Западная Виргиния (США) в семье инженера-электрика и школьной учительницы. Джон не был выдающимся учеником, а математику и вовсе не любил. Но всё изменилось после того, как Джон прочитал книгу «Творцы математики».
Своё образование Джон Нэш продолжил в Политехническом институте Карнеги. Там он окончательно сделал выбор в пользу математики. Успехи в учёбе в институте были настолько выдающимися, что по окончании института Нэш получил сразу две степени — бакалавра и магистра и поступил в Принстонский университет. Там произошло знакомство Джона Нэша с теорией игр[1].
Это новое направление так заинтересовало математика, что уже в 1949 году в 21 год он написал диссертацию о теории игр, создав основы научного метода, повлиявшего на развитие мировой экономики. Через 45 лет в 1994 году Джон Нэш был удостоен Нобелевской премии в области экономики «За анализ равновесия в теории некооперативных игр».
В этой работе учёный доказал существование равновесия — набора в игре для двух и более игроков, в котором ни один участник не может увеличить выигрыш, изменив свою стратегию, если другие участники своих стратегий не меняют — в смешанных стратегиях в любой конечной игре.
Равновесие по Нэшу широко используется в самых различных областях — экономике (например, политика ценообразования), в естественных науках (например, исследование модели хищник—жертва), в социологии (теория рационального выбора), политологии, военном деле (концепция взаимного гарантированного уничтожения) и так далее.
Кроме теории игр, Нэш работал и в области теории нелинейных дифференциальных уравнений. И в 2015 году был удостоен высшей награды по математике — Абелевской премии. Эту награду он получил за достижения в «чистой математике». Джон Нэш изучал изометрические вложения, сформулировал две теоремы, которые в современной математике считаются классическими. Говоря простым языком, Нэш нашёл способы преобразовать абстрактную многомерную поверхность в трёхмерную евклидову с сохранением измерений.
Задача эта решается с помощью дифференциальных уравнений в частных производных, чем и занимался Нэш. До него решение таких уравнений считалось невозможным. Однако Нэш разработал способ решать такие уравнения. В настоящее время такие уравнения используются как в геометрическом анализе, так и в физике.
Джон Форбс Нэш-младший — единственный в настоящее время учёный, получивший две премии — Нобелевскую и Абелевскую.
1 Теория игр — математический метод изучения оптимальных стратегий в играх, раздел прикладной математики, а именно, исследования операций.

Острогра́дский, Михаи́л Васи́льевич
Родился 24 сентября 1801 года — умер 1 января 1862 года
Михаил Васильевич Остроградский — российский учёный, математик и механик, признанный лидер математиков Российской империи — родился в Полтавской губернии Российской империи в семье помещика. Начал своё обучение Михаил в Полтавской гимназии, был вольным слушателем, а затем и студентом Харьковского университета. В 1818 году Остроградский успешно дал экзамены за трёхлетний курс университета, а в 1820 году — экзамены на степень кандидата наук. Но часть профессоров университета была настроена против него и Остроградского лишили и аттестата кандидата наук, и диплома об окончании университета.
Но будущий учёный не остановился. В 1822 году он прибыл во Францию, где обучался в Сорбонне, Коллеж де Франс, посещая лекции таких учёных, как Лаплас, Фурье, Коши, Ампер. Основным научным направлением Остроградский для себя определил прикладную математику, то есть то, что можно применить на практике.
В 1826 году Михаил Остроградский подготовил свою первую научную работу «о распространении волн в цилиндрическом бассейне», которая была позже опубликована.
В конце 1927 года талантливый учёный приехал в Петербург. Он был профессором таких учебных заведений, как Главное Инженерное училище Российской империи, Институт Корпуса инженеров путей сообщения, Николаевская инженерная Академия, Морской кадетский корпус, Главное артиллерийское училище, Главный педагогический институт и многих других.
В области математического анализа Остроградскому принадлежат:
- формулы преобразования интеграла по объёму в интеграл по поверхности
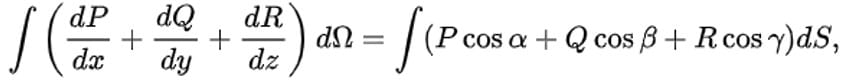
где cos α dS = dydz, cos β dS = dzdx, cos γ dS = dxdy, ω = dΩ — элемент объёма, s = dS — элемент поверхности;
- понятия сопряжённого дифференциального оператора, вариации кратного интеграла;
- правила преобразования переменных интегрирования в двойных и тройных интегралах;
- метод интегрирования рациональных функций с помощью выделения рациональной части интеграла
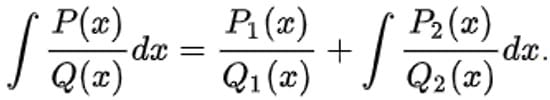
и многое другое.
Кроме математического анализа, Михаил Остроградский внёс вклад в развитие теоретической механики, математической физики, теории чисел, алгебры, теории вероятностей.
Также Михаил Васильевич приложил немало сил к совершенствованию преподавания курсов математики в учебных заведениях, писал учебники по высшей и элементарной математике, содействовал изданию трудов Леонарда Эйлера, Карла Фридриха Гаусса.
А вот работы Николая Ивановича Лобачевского Остроградский не понял и не признал.

Паска́ль, Блез
(фр. Blaise Pascal)
Родился 19 июня 1623 года — умер 19 августа 1662 года
Выдающийся французский учёный, математик, физик, философ родился во французском городе Клермон-Ферран. Его отец Этьен Паскаль интересовался математикой и науками и уделял большое внимание образованию своих детей, особенно сына. Блез достаточно рано начал проявлять математические способности. Так, в 11 лет он написал свой первый труд — заметку о звучании вибрирующих тел. Позже самостоятельно, без учебников, доказал первые теоремы Евклида, в том числе теорему о сумме углов в треугольнике.
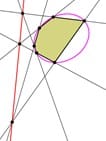
В 16 лет Блез Паскаль написал, используя работы Дезарга о конических сечениях, небольшую работу «Мистическая гексаграмма». Эта работа — основа теоремы Паскаля: если шестиугольник вписан в окружность (или в любое другое коническое сечение — эллипс, параболу, гиперболу, в пару прямых), то точки пересечения трёх пар противоположных сторон лежат на одной прямой — прямой Паскаля (рис. 1). Теорема Паскаля была его первым математическим открытием и важным вкладом в проективную геометрию.
В 1642 году Б. Паскаль, чтобы помочь своему отцу, создаёт первую счётную машину — паскалину (рис. 2). Это устройство, использующее специальные кольца, позволяло выполнять сложение и вычитание даже с шестизначными числами.

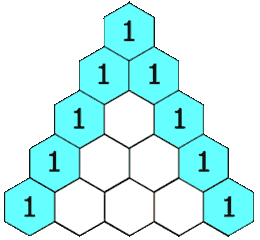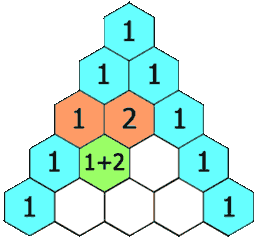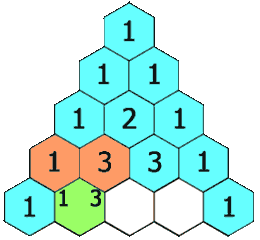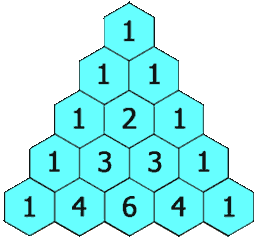
В 1653 году был опубликован «Трактат об арифметике треугольника», в котором Паскаль описал представление коэффициентов бинома (a + b)n в виде таблицы. Это представление названо «треугольником Паскаля» (рис. 3). Позже, совместно с Пьером де Ферма, фактически закладывают основы математической теории вероятностей. Также, опираясь на их работы, Готфрид Вильгельм Лейбниц получает формулу исчисления бесконечно малых.
Именем Блеза Паскаля был назван созданный Никлаусом Виртом в 1968–1969 годах язык программирования Pascal.

Пифаго́р Са́мосский
(др.-греч. Πυθαγόρας ὁ Σάμιος, лат. Pythagoras)
По разным данным родился в 570 году до нашей эры — умер в 495 году до нашей эры
Пифагор — древнегреческий философ, математик, теоретик музыки и мистик, создатель религиозно-философской школы пифагорейцев. Достоверных сведений о происхождении и жизни Пифагора, как и о других древних учёных, мало. Принято считать, что Пифагор родился на острове Самос, который расположен в восточной части Эгейского моря. В молодости много путешествовал и учился, посещал Египет, Заратуштру, Крит. В возрасте 40 лет Пифагор покинул Самос и через некоторое время остался жить в Италии. Там он основал собственную школу пифагорейцев.
Помимо философии, Пифагор внёс большой вклад в развитие математики. С его именем связывают:
- ведение доказательств;
- дедуктивное построение геометрии прямолинейных фигур;
- создание учения о подобии, построение некоторых многоугольников и многогранников;
- понятия чётных и нечётных, простых и составных чисел;
- основные положения теории об арифметических прогрессиях и гармонических средних.
Самым известным утверждением является теорема Пифагора: квадрат гипотенузы прямоугольного треугольника равен сумме квадратов его катетов. Изначально же эта теорема имела другую формулировку: квадрат, построенный на гипотенузе, равновелик[1] сумме квадратов, построенных на катетах (рис. 1).
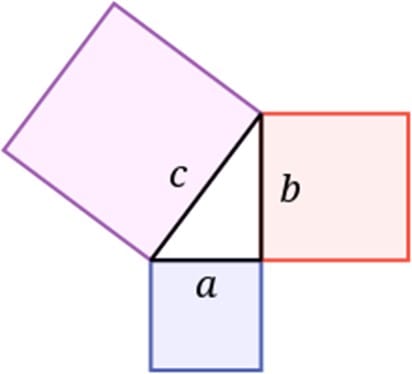
Наглядное доказательство теоремы Пифагора
1 Равновеликие фигуры — это фигуры, которые имеют одинаковую площадь.

Пуанкаре́, Жуль Анри́
(фр. Jules Henri Poincaré)
Родился 29 апреля 1854 года — умер 17 июля 1912 года
Пуанкаре — величайший французский математик, физик, астроном, философ. Работал на стыке наук, используя математические методы вычислений для физики, астрономии, геометрии. Жуль Анри Пуанкаре являлся членом более 30 академий мира, в том числе главой Парижской академии наук. Автор более 500 научных работ.
Отец Жуля был профессором медицины, поэтому он получил хорошую домашнюю подготовку, что позволило поступить сразу на второй курс лицея. Далее уже в студенческие годы Пуанкаре начал проводить исследования и публиковаться. Его первой опубликованной работой была статья по дифференциальной геометрии. По завершении обучения он защитил диссертацию, которая содержала материал на несколько таких работ. Далее занимался преподавательской деятельностью.
Самые значимые достижения связаны с созданием топологии, созданием качественной теории дифференциальных уравнений, разработкой автоморфных функций, созданием математической основы теории относительности, созданием наглядной модели геометрии Лобачевского. Пуанкаре создал новый раздел математики, который получил название качественной теории дифференциальных уравнений. Он разработал метод получения важной информации, не решая уравнение, а лишь рассматривая семейство решений.
Пуанкаре вывел разложение автоморфных функций в ряды, доказал теорему об униформизации алгебраических кривых, представляя их через автоморфные функции, что решило 22 проблему Гильберта[1].
Работая в области топологии, Пуанкаре развил и обогатил науку своими дополнениями. В этих дополнениях содержалась знаменитая гипотеза Пуанкаре, которая была доказана лишь почти век спустя в 2002 году российским математиком Григорием Перельманом.
Великий учёный имеет множество званий и наград, в науке много терминов получили его имя, а его исследования и весомый вклад в науку сложно переоценить.
1 Проблемы Гильберта — список из 23 кардинальных проблем математики, который Давид Гильберт представил на II Международном конгрессе математиков в Париже в 1900 году. 12 проблем из этого списка к настоящему времени решены, для некоторых есть частичное решение.