
А́бель, Нильс Хе́нрик
(норв. Niels Henrik Abel)
Родился 5 августа 1802 года — умер 6 апреля 1829 году
Нильс Абель родился в городе Финнёй (Норвегия) в многодетной семье, отец его был пастором. Ещё в школьные годы Нильс проявлял высокие способности в математике.
Несмотря на непродолжительную жизнь, Нильс Абель оставил после себя богатое научное наследие.
Он работал в разных областях математики, брался за исследование сложных задач, не имевших на тот момент решения. Так, например, Абель нашёл условие, при котором корень уравнения выражался в радикалах через коэффициенты этого уравнения, и показал на примерах, что в уравнениях пятой степени в некоторых случаях корни так выразить нельзя. Статья на данную тему опубликована лишь в 1826 году.
Среди открытий Абеля стоит выделить большое количество математических теорем. В 1823 году учёным был написан важный труд, посвящённый интегрируемости дифференциальных уравнений. Так же Абель работал в области исследования некоторых алгебраических функций, что послужило открытию им теории гиперэллиптических функций. Немало важных открытий Абелем сделано в области теории рядов.
В 2002 году правительством Норвегии основана Абелевская премия, вручаемая математикам за выдающиеся исследования. Абелевская премия является аналогом Нобелевской[1], ведь последняя в области математики не вручается.
В Норвегии в городах Ерстаде и Осло установлены памятники великому математику.
1 Нобелевская премия — наиболее престижная международная премия в области науки, литературы и общественной деятельности.

Аль-Хорезми́, Абу́ Абдулла́х Муха́ммад ибн Муса́
(перс. بن موسی خوارزمی, араб. أبو عبد الله محمد بن موسی الخوارزمی)
Родился приблизительно в 783 году — умер приблизительно в 850 году
Персидский учёный IX века из Хорезма, математик, астроном, географ и историк. О его жизни известно очень мало, поскольку он о себе ничего не писал. Узнать о нём можно только из того, что о нём писали другие.
Родился Аль-Хорезми в Хиве, обучение начал дома, изучал греческую и индийскую науку. В 819 году Аль-Хорезми приехал в Багдад, где провёл большую часть своей жизни. Там он возглавлял «Дом мудрости».
Аль-Хорезми разработал правила выполнения четырёх арифметических действий. И эти правила — это самый простой пример математических алгоритмов.
Самой известной работой Аль-Хорезми считается «Книга восполнения и противопоставления» (рис. 1). Там впервые встречается термин «Алгебра» — «аль-джебр». Сам термин «аль-джебр» (восполнение) означает операцию, состоящую в переносе отрицательных членов из одной части уравнения в другую, чтобы в обеих частях уравнения все члены стали положительными. Ещё одно понятие данной работы — «аль-мукабала» (противопоставление) — это приведение подобных членов.

В этом труде изложены основы арифметики в десятичной системе счисления, классификации линейных и квадратных уравнений с методами их решения.
Используемая десятичная система счисления получила распространение благодаря книге Аль-Хорезми «Об индийском счёте».
Аль-Хорезми изготовил инструмент для измерения объёма и длины окружности Земли и с достаточно высокой точностью измерил длину радиуса дуги земного меридиана.
Составил подробные тригонометрические таблицы, которые содержали значения основных тригонометрических функций.
Аль-Хорезми, изучив дошедшие до него математические сведения, впервые представил алгебру как науку, изучающую общие методы решения линейных и квадратных уравнений, и классифицировал данные уравнения.

Архиме́д
(др.-греч. Ἀρχιμήδης)
Родился в 287 году до нашей эры — умер в 212 году до нашей эры
Древнегреческий учёный родился и большую часть жизни прожил в городе Сиракузы на острове Сицилия. Математику Архимед изучал дома со своим отцом. Позже Архимед получил возможность переехать в Александрию, чтобы учиться в знаменитой Александрийской библиотеке. После окончания обучения Архимед вернулся в Сиракузы.
За всю жизнь Архимед написал достаточно много научных трудов, часть из которых относится к математике.
Архимед описал плоскую кривую, которую позже назвали его именем — спираль Архимеда (рис. 1). В стереометрии Архимед исследовал полуправильные выпуклые многогранники, которые называются «архимедовыми телами».
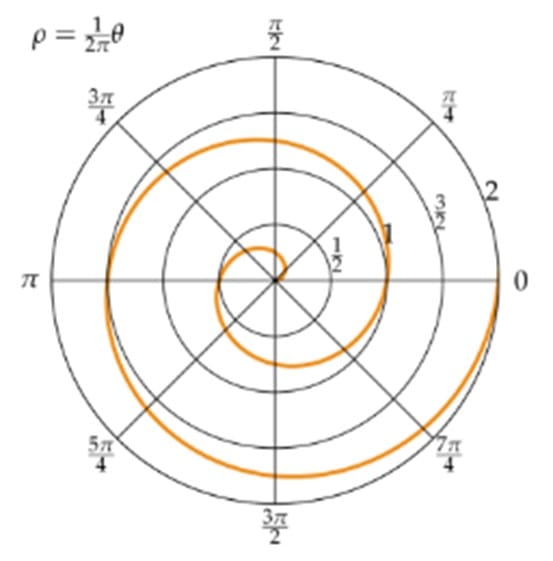
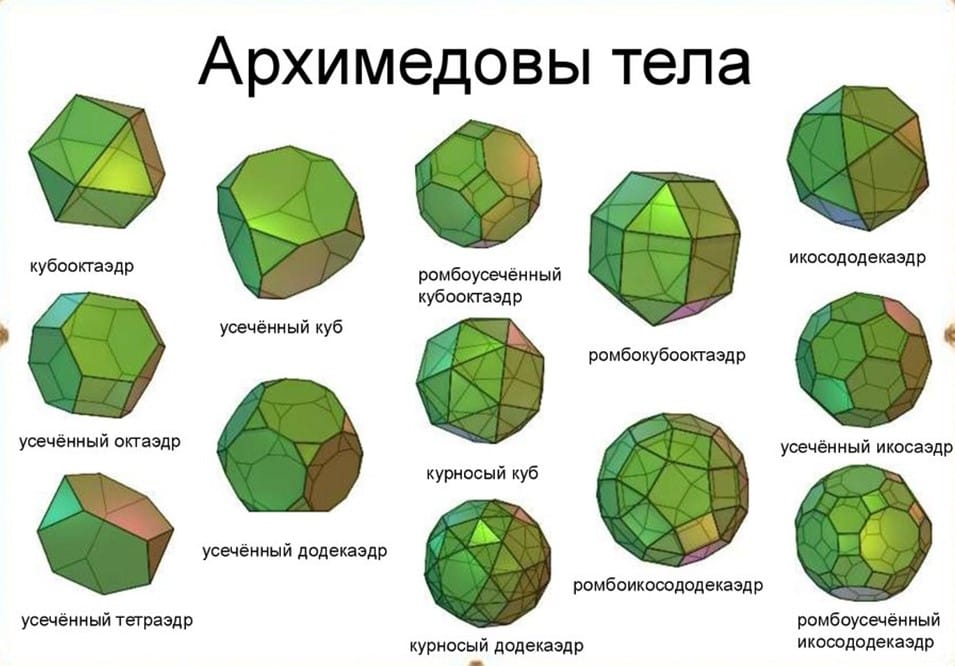
Архимед нашёл общий метод вычисления площадей фигур и поверхностей (круга, сегмента шара, витка спирали Архимеда), объёмов таких тел, как конус, шар, сегмент шара, цилиндр, эллипсоид, параболоид, двуполостный гиперболоид вращения, используя для этого бесконечно малые[1]. В работе «Квадратура параболы» с помощью суммы бесконечного ряда Архимед доказал, что площадь сегмента параболы, отсекаемого от неё прямой, составляет 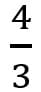 от площади вписанного в этот сегмент треугольника (рис. 3):
от площади вписанного в этот сегмент треугольника (рис. 3):
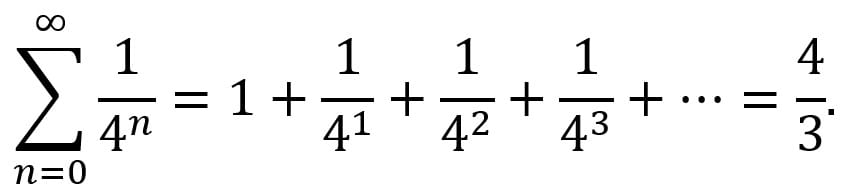
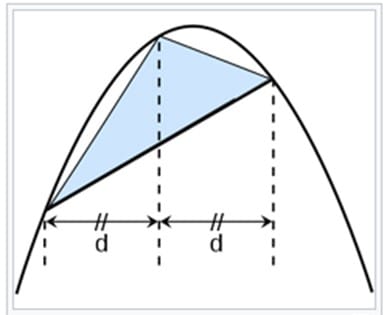
Архимед показал, что объёмы конуса и шара, вписанных в цилиндр, и самого цилиндра соотносятся как 1:2:3.
Архимед первым установил связь задач на нахождение экстремумов с задачами определения касательных и показал, как решать подобные задачи.
Общий метод определения касательной в любой точке кривой, найденный Архимедом, стал основой дифференциального исчисления.
В работе «Об измерении круга» Архимед описал приближение для числа π — архимедово число 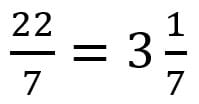 и оценил точность этого приближения:
и оценил точность этого приближения: 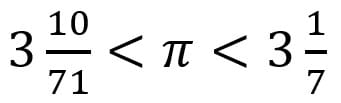 . Для этого он использовал круг и вписанные и описанные n-угольники (рис. 4).
. Для этого он использовал круг и вписанные и описанные n-угольники (рис. 4).
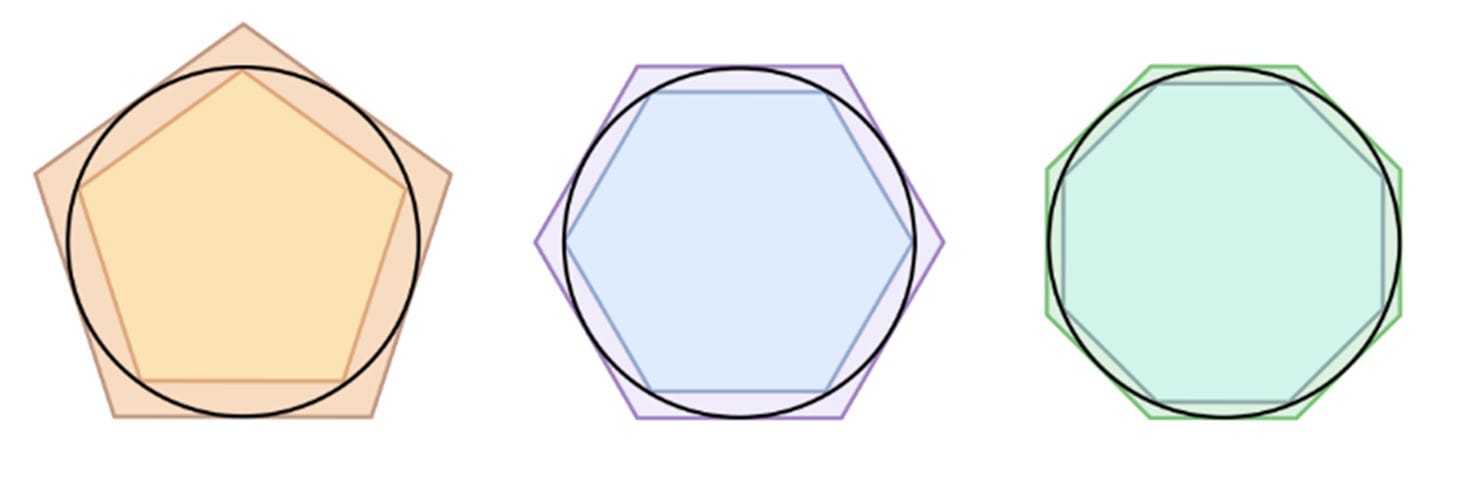
Аксиома Архимеда: «Если имеются две величины, a и b, и a меньше b, то, взяв a слагаемым достаточное количество раз, можно превзойти b: 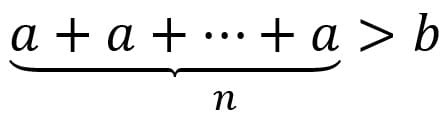 ».
».
1 Бесконечно малая — это величина, последовательность или функция, предел которой равен нулю.

Берну́лли, Дании́л
(нем. Daniel Bernoulli)
Родился 29 января 1700 года — умер 17 марта 1782 года
Родился Даниил Бернулли в Гронингене, город в Голландии. Бернулли — физик и математик (по образованию медик), является одним из основателей математической физики [1]. Его отец и старший брат также были математиками, у которых Даниил учился математике.
Его самые известные труды — это «Математические этюды», «Замечания о рекуррентных последовательностях» и «Гидродинамика». В последнем наряду с другими исследованиями и открытиями содержится известный «закон Бернулли».
Закон Бернулли. Величина 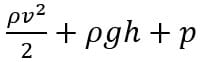 сохраняет постоянное значение вдоль линии тока:
сохраняет постоянное значение вдоль линии тока:
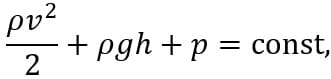
где ρ — плотность жидкости; v — скорость потока; h — высота; p — давление; g — ускорение свободного падения.
Данный закон наглядно показывает, чем занимался Бернулли в математической физике: разработкой математических моделей для физических явлений. Закон Бернулли имеет широкое применение в различных научных областях.
Даниил также занимался теорией вероятностей, теории рядов, численными методами и дифференциальными уравнениями. Он первый применил математический анализ к задачам теории вероятностей. Бернулли также внёс весомый вклад в математическую статистику, для ряда практически важных задач с применением вероятностных методов. Так, например, он вычислил количество людей, заболевших оспой, и их смертность с целью показать действенность вакцины.
Бернулли внёс вклад и в математический анализ, вычислив предел[2] выражения 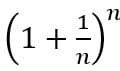 , при этом получив число e = 2,718… (основание натурального логарифма).
, при этом получив число e = 2,718… (основание натурального логарифма).
Даниил Бернулли был великим математиком и физиком, который объединил эти две науки. Умер он в городе Базель (Швейцария).
1 Математическая физика — наука о математических моделях физических явлений.
2 Предел выражения
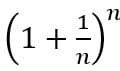 — это второй замечательный предел.
— это второй замечательный предел.
Буль, Джордж
(англ. George Boole)
Родился 2 ноября 1815 года — умер 8 декабря 1864
Английский математик, родившийся в городке Линкольн на востоке Англии, считается основоположником математической логики, хотя сам логику не причислял к математическим наукам.
Занимался он и другими областями математики, в частности теорией инвариантов,[1], статистикой и теорией вероятностей, причем в каждую из них внёс весьма существенный вклад.
Булем было написано и опубликовано большое количество трудов (более 50), наиболее известные из которых «Математический анализ логики», «Логическое исчисление», «Исследование законов мышления».
«Законы мышления» были написаны после того, как Буль решил рассматривать высказывания и суждения древних философов, таких как Аристотель и его последователей на языке алгебры. Джордж не хотел заниматься лишь нахождением математических методов для решения теоретических задач, он хотел найти математические законы, описывающие разум.
В своих исследованиях Джордж Буль принимал совокупность объектов за единицу, буквами — выборки из неё, связанные с обычными прилагательными и существительными. Например, за x принимались «рогатые», а за y — «овцы», последовательный выбор x и y из единицы даст класс рогатых овец.
Буль показывал, что все рассуждения в логике сводятся к определению истинности или ложности в данных рассуждениях. Предложил ложь обозначать нулём, истину — единицей. Тем самым связал логику с алгеброй воедино. Буль также описал математические законы и операции, которым подчинялась новая наука. Булева алгебра (рис. 1) как подраздел математической логики не нашла применения у математиков того времени, вплоть до середины XX века.
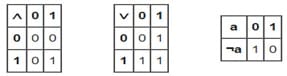
Буль, не оценённый своими современниками, в настоящем времени считается прародителем искусственного интеллекта и учёным, заложившим основу для современного информационно-цифровизированного общества.
1 Инвариант — величина или свойство, не изменяющиеся после каких-либо преобразований.

Ве́йерштрасс, Карл Те́одор Вильге́льм
(нем. Karl Theodor Wilhelm Weierstraß)
Родился 31 октября 1815 года — умер 19 февраля 1897 года
Выдающийся немецкий математик, лучший преподаватель Германии, «отец современного анализа» родился в Остенфельде (Пруссия, часть современной Германии) в семье чиновника. Семья Вейерштрассов относилась к интеллектуальным, дети изучали иностранные языки. Карл считался одним из лучших учеников падерборнской гимназии. Карл по настоянию отца сначала пошёл учиться на юриста, но образование не закончил — не ходил на лекции, а самостоятельно изучал математику. Позже Карл Вейерштрасс, прослушав курс лекций по математике в университете Мюнстера, успешно сдал экзамен, дающий право читать лекции, и следующие 14 лет проработал учителем, параллельно (по ночам) занимаясь научной работой.
Первая работа Вейерштрасса была опубликована в 1853 году, а уже в 1854 году за работу по абелевым функциям Кёнингсбергский университет присудил Карлу степень почётного доктора без защиты.
В 1856 году учёный переезжает в Берлин. С этого времени он становится всё больше популярным в международном научном сообществе. Значимость работ Вейерштрасса невозможно недооценить. Он выстроил фундамент математического анализа, дал ему строгое логическое обоснование. А для этого построил теорию действительных (вещественных) чисел на языке ε-δ. Определения таких понятий, как функция, непрерывная в точке, предел функции, сходимость ряда, равномерная сходимость функции, базовые теоремы и многое другое используются в настоящее время без изменений.
Определение. Функция f(x) непрерывна в точке x = x0, если для любого сколь угодно малого числа ε > 0 существует такое число δ, что если | x − x0 | < δ, то | f (x) − f (x0) | < ε.
Вейерштрасс доказал возможность представления непрерывной функции с помощью равномерно сходящегося степенного ряда. Кроме этого, у него было много работ в теории эллиптических и абелевых функций, теории целых функций и функций нескольких комплексных переменных. Также учёный создал теорию делимости степенных рядов.
Современному виду вариационное исчисление также обязано Карлу Вейерштрассу.
В геометрии он создал теорию минимальных поверхностей, внёс вклад в теорию геодезических линий. В линейной алгебре им разработана теория элементарных делителей.
Вейерштрасс доказал, что поле,[1] комплексных чисел — единственное коммутативное расширение поля действительных чисел без делителей нуля.
Собрание сочинений Карла Вейерштрасса насчитывает семь томов, три из которых — его работы, а остальные — обработка его лекций, которые считаются педагогическими шедеврами.
1 Поле в математике — это множество, в котором сложение, вычитание, умножение и деление определены и ведут себя так же, как соответствующие действия с действительными числами.

Вие́т, Франсуа́
(фр. François Viète, seigneur de la Bigotière)
Родился в 1540 году — умер в 1603 году
Французский математик (хотя математику считал хобби) родился в 1540 году во Франции в городе Фонтене-ле-Конт, по образованию и основной профессии был юристом.
Франсуа Виет считается одним из основоположников символьной алгебры. До него решение уравнений было очень сложным в виде длинных словесных рассуждений и трудновыполнимых действий. Виет же предложил использовать упрощённую символику: неизвестные в уравнении были обозначены гласными буквами, а коэффициенты — согласными. Таким образом, Виет ввёл в алгебру запись математических формул.
Другими известными открытиями учёного являются:
- полное аналитическое изложение теории уравнений первых четырёх степеней;
- идея применения трансцендентных функций,[1] к решению алгебраических уравнений;
- оригинальный метод приближённого решения алгебраических уравнений;
- частичное решение о построении круга.
Но самым известным научным достижением Франсуа считаются знаменитые «формулы Виета» для коэффициентов многочлена как функций его корней. Причём «формулы Виета», используемые в современных школах для квадратного уравнения, применялись ещё до рождения учёного. Франсуа же показал, что такими свойствами обладают корни уравнений любой степени.
Теорема Виета.
Сумма корней приведённого квадратного уравнения x2 + px + q = 0 равна (−p), а произведение корней равно q.
Пример.
Найдём корни уравнения x2 + x − 6 = 0.
Решение.
Обозначим корни x1 и x2.
По теореме Виета имеем: x1 + x2 = −1; x1 · x2 = −6.
Так как 2 + (−3) = −1 и 2 · (−3) = −6, то корнями уравнения x1 и x2 могут быть только числа 2 и −3.
Ответ: {−3; 2}.
1 Трансцендентные функции — все неалгебраические функции: показательная, логарифмическая, тригонометрические, обратные тригонометрические функции.

Галуа́, Эвари́ст
(фр. Évariste Galois)
Родился в 1811 году — умер в 1832 году
Родился Эварист Галуа во Франции, в предместье Парижа. Эварист за свою непродолжительную жизнь сделал многое в области математики, а именно в алгебре. В двенадцатилетнем возрасте Галуа поступил в королевский коллеж, но лишь в шестнадцать он увлёкся математическими трудами других учёных. В частности, после прочтения сочинения Нильса Абеля о решении уравнений произвольной степени, он увлёкся данной темой и решил провести собственное исследование.
Эварист Галуа вместе с тем, что являлся блестящим математиком, выдвинул прогрессивные идеи в алгебре, также был республиканцем и участвовал в политических выступлениях, что печально сказывалось на его репутации: из-за этого был исключён из высшего учебного заведения, где проучился лишь год, попав в тюрьму.
Опубликованных работ у Галуа мало, но в них изложена его теория.
Теория Галуа — это раздел алгебры, позволяющий переформулировать определённые вопросы теории полей на языке теории групп, делая их в некотором смысле более простыми.
Эварист Галуа сформулировал основные утверждения этой теории в терминах перестановок корней заданного многочлена (с рациональными коэффициентами); он первый описал множества перестановок, при этом использовал термин «группа», множества замкнутого относительно композиции и содержащего тождественную перестановку.
Эварист Галуа за 4 года увлечённости математикой сделал важные открытия, которые не были оценены его современниками, но по прошествии некоторого времени произвели огромное впечатление на потомков и положили начало новому направлению в алгебре.
Погиб Галуа в 1832 году в Париже на дуэли в возрасте 20 лет.

Га́усс, Иога́нн Карл Фри́дрих
(нем. Johann Carl Friedrich Gauß)
Родился 30 апреля 1777 года — умер 23 февраля 1855 года
Гениальный учёный — математик, физик, геодезист, астроном, родился в Брауншвейге (Германия). Уже в раннем возрасте Гаусс проявлял себя как незаурядный ребёнок. При том, что родился и рос в малообразованной семье, в три года он умел писать и считать.
Гаусс поступил, учился и окончил университет в Брауншвейге по направлению математика, хотя сначала выбирал между математикой и филологией, так как хорошо владел языками французским, английским, латинским, изучал русский язык.
Гауссу принадлежат некоторые значимые открытия в теории чисел, сделанные им ещё в студенческие годы, например, доказательство закона взаимности квадратичных вычетов.
Карл Гаусс доказал возможность построения правильных многоугольников (n-угольников) с помощью циркуля и линейки, найдя условия построения:
- если n — простое число, то оно имеет вид n = 22k + 1 (число Ферма);
- если n — составное число, то n = 2kp1…pm, где pi — различные простые числа Ферма.
Гаусс делал много открытий, но часть из них не публиковал, так как считал не до конца разработанными, поэтому его часто опережали коллеги.
В своей диссертации Гаусс впервые доказал основную теорему алгебры,[1]. Позже он предложил ещё четыре различных доказательства.
В астрономии Гаусс применил новые, разработанные им, математические методы расчётов нахождения планет. В геодезии так же, как и в астрономии, Гаусс предлагает новые математические вычислительные методы для проведения геодезической съёмки. Здесь он использует практическое применение своего метода наименьших квадратов. Гаусс работает над теорией поверхностей, где появляется понятие «гауссова кривизна» (рис. 1). Из этой работы Гаусса зарождается дифференциальная геометрия.
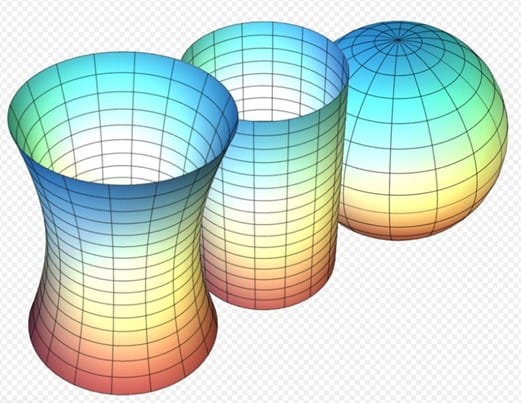
гиперболоид (отрицательная), цилиндр (нулевая), сфера (положительная)
Гаусс провёл исследование гипергеометрического ряда, обобщающего разложение практически всех известных тогда функций. Открыл гауссовы комплексные целые числа, с помощью которых доказывал важные арифметические теоремы и для комплексных, и для вещественных чисел.
Гаусс был величайшим учёным в различных областях науки, сделавшим множество различных открытий, которые используются в современности. После смерти Гаусса была отчеканена медаль с его портретом и надписью «Король математиков».
1 Основная теорема алгебры — в современном мире не является основной, получила такое название, когда главным направлением алгебры был поиск решений алгебраических уравнений.

Ги́льберт, Дави́д
(нем. David Hilbert)
Родился 23 января 1862 года — умер 14 февраля 1943 года
Немецкий математик, работавший в различных её областях (теория инвариантов, теория алгебраических чисел, геометрия, математическая физика, теория интегральных уравнений и некоторые другие), родился 23 января 1862 года в пригороде Кёнигсберга (сейчас посёлок Знаменск, Калининградская область). Главными достижениями считаются разработка полной аксиоматики евклидовой геометрии и теории гильбертовых пространств. Данные работы впоследствии станут общепризнанными классическими фундаментальными теориями математики.
Давид Гильберт получил математическое образование в Кёнигсбергском университете, где позже преподавал, защитив диссертацию по теории инвариантов. Считался блестящим преподавателем.
У Гильберта вышло в печать много трудов, которые переведены на различные языки, в том числе и на русский. К наиболее известным работам относятся «Отчёт о числах», «Основания геометрии». Гильберту принадлежит знаменитый список двадцати трёх не решённых кардинальных проблем математики того времени, которые задали направление исследований математикам.
Гильберт создал теорию о гильбертовых пространствах, которая обобщает евклидовы пространства на бесконечный случай, что послужило становлению функционального анализа в современном виде.
Гильбертом были выдвинуты требования к аксиоматической теории: непротиворечивость, полнота, независимость аксиом. Таким образом, Гильберт считал, что необходима полная формализация математики. Гильберт разработал строгую логическую теорию доказательств, с помощью которой непротиворечивость математики свелась бы к доказательству непротиворечивости арифметики. Данные рассуждения Гильберта подвергались критике другими выдающимися математиками того времени, иногда не без основания. Но тем не менее разработанная программа Гильберта в двух томах «Основания математики» стала стимулом в развитии математической логике.