
Д’Аламбер Ж. 
Дедекинд Р. 
Декарт Р. 
Дирихле Г. 
Евклид 
Кантор Г. 
Кардано Дж. 
Клейн Ф. 
Ковалевская С. 
Колмогоров А. 
Коши О.

Д’Аламбер, Жан Лерон
(фр. Jean Le Rond D’Alembert)
Родился 16 ноября 1717 года — умер 29 октября 1783 года
Французский учёный, математик, механик, философ родился в Париже. Воспитывался приёмными родителями. Своё обучение Жан Лерон начал с четырёх лет, когда его отдали в пансион. Затем он получил звание бакалавра искусств, окончив колледж имени Мазарини, звание лиценциата прав, окончив двухгодичную академию юридических наук. Также Жан Лерон начинал изучать медицину. Но математика притягивала его.
В 1746 году Д’Аламбер опубликовал «Исследования по интегральному исчислению», где привёл первое, нестрогое доказательство основной теоремы алгебры[1]. Окончательное доказательство принадлежит Карлу Гауссу.
В 1747 году в статье по теории поперечных колебаний струн учёный привёл метод решения дифференциального уравнения второго порядка в частных производных, а также получил значимые результаты в теории обыкновенных дифференциальных уравнений с постоянными коэффициентами, ввёл понятие предела.
В 1768 году Д’Аламбер установил достаточный признак сходимости числовых рядов, который в настоящее время носит его имя.
Признак Д’Аламбера сходимости числовых рядов.
Если для числового ряда 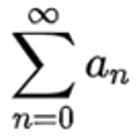 существует такое число q, 0 < q < 1, что, начиная с некоторого номера, выполняется неравенство
существует такое число q, 0 < q < 1, что, начиная с некоторого номера, выполняется неравенство 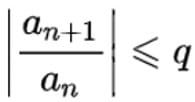 , то данный ряд сходится абсолютно. Если, начиная с некоторого номера
, то данный ряд сходится абсолютно. Если, начиная с некоторого номера 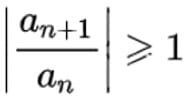 , то ряд расходится.
, то ряд расходится.
В 1752 году при изучении задач гидродинамики для решения дифференциального уравнения с частными производными эллиптического типа Жан Лерон Д’Аламбер первый использовал функции комплексного переменного[2].
В работах Д’Аламбера, как и у Леонарда Эйлера, можно встретить уравнения, которые для аналитической функции связывают её действительную и мнимую части. В настоящее время эти уравнения известны как условия Коши—Римана.
В теории обыкновенных дифференциальных уравнений с постоянными коэффициентами и систем таких уравнений первой и второй степени также присутствуют важные результаты, полученные Жаном Лероном.
Кроме того, в его трудах встречаются рассуждения о теории вероятностей.
В честь Д’Аламбера назван кратер на обратной стороне Луны.
1 Основная теорема алгебры — теорема о существовании корней алгебраического уравнения.
2 Функция комплексного переменного — f(z) = f(x + iy), где x, y ∈ R, i2 = −1.

Дедеки́нд, Ю́лиус Вильге́льм Ри́хард
(нем. Julius Wilhelm Richard Dedekind)
Родился 6 октября 1831 года — умер 12 февраля 1916 года
Дедекинд — немецкий математик, работающий и привнёсший огромный вклад в области алгебры и теории чисел. Родился в семье профессора-юриста. Получил образование и работал в университете родного Брауншвейга. Ученик, последний аспирант Карла Гаусса, однокурсник Бернхарда Римана.
Математикой увлекался с ранних лет, после поступления в университет сразу стал проводить исследования и публиковать свои работы. По окончании университета некоторое время преподавал и Гёттингене.
В 1852 году Рихард Дедекинд защитил диссертацию по теории интегралов Эйлера, за что получил докторскую степень. Но наибольший вклад он внёс в алгебру, теорию чисел, теорию множеств.
Он первый предложил понятие множества в математике, определил более точное значение числа Эйлера, разработал теорию идеалов. Также ввёл абстрактные алгебраические понятия кольца и модуля. Дедекинд разработал аксиоматический метод для систем натуральных чисел. Позже данный метод был принят как основополагающий в математике. В теории чисел Дедекинд провёл важное исследование, которое описал в статье «Начала теории иррациональных чисел», где впервые ввёл понятие среза для определения действительных чисел.
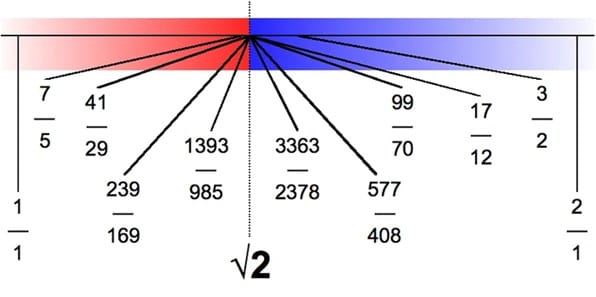
Теорема (принцип, аксиома) Дедекинда о непрерывности числовой прямой: для всякого сечения А|В множества действительных чисел существует действительное число α, которое является либо наибольшим в классе А, либо наименьшим в классе В. Число α является верхней гранью множества А и нижней гранью множества В (рис. 1).
Рихард Дедекинд встречался, был знаком, сотрудничал со многими великими математиками, такими, как Карл Вейерштрасс, Георг Кантор, Петер Густав Лежён Дирихле.
Дедекинд оказал огромное влияние на развитие математики, заложил фундамент для дальнейших исследований и разработки новых теорий.

Дека́рт, Рене́
(фр. René Descartes)
Родился 31 марта 1596 года — умер 11 февраля 1650 года
Французский математик и философ родился в городе Лаэ (сейчас носит название Декарт), провинция Турень, в семье судьи.
«Рассуждение о методе» — это главный философско-математический труд французского учёного, состоящий из нескольких приложений. Декарт является основоположником аналитической геометрии, в ней он связал алгебру и геометрию между собой.
Рене Декарт продолжил работу Франсуа Виета по введению в математику символьных обозначений. Так, в уравнениях он обозначал коэффициенты латинскими буквами a, b, c, d,…, а неизвестные — x, y, z,… ввёл в использование современный вид показателя степени, а над подкоренным числом он предложил ставить черту.
Французский учёный разрабатывал канонические уравнения. С помощью таких уравнений 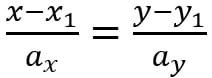 можно задать в прямоугольной системе координат на плоскости прямую, которая имеет направляющий вектор
можно задать в прямоугольной системе координат на плоскости прямую, которая имеет направляющий вектор 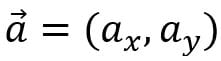 и проходит через точку M1(x1,y1).
и проходит через точку M1(x1,y1).
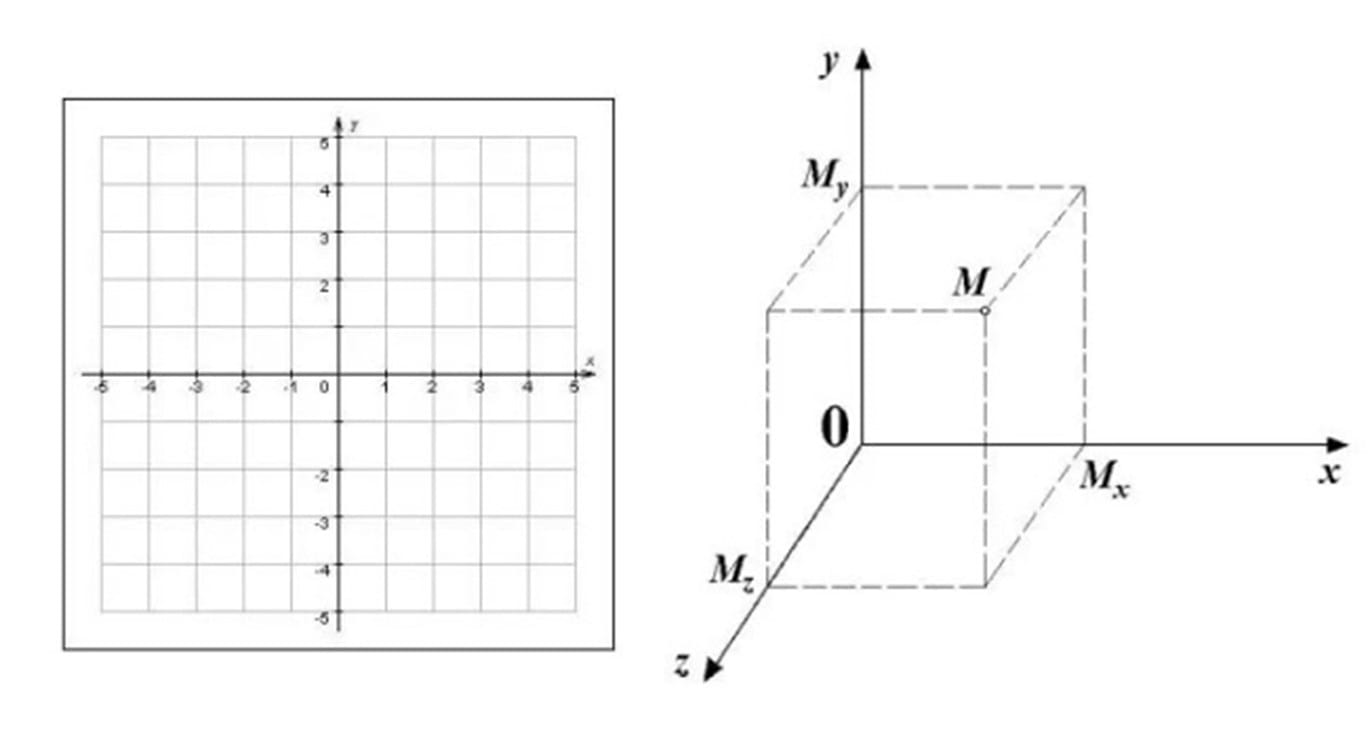
Рене Декарт внёс большой вклад в совершенствование математики и физики, придумав современную прямоугольную систему координат (рис. 1), названную в последствии декартовой. Он использовал её для того, чтобы стало возможным описать геометрические свойства кривых и тел, используя классическую алгебру. Благодаря этому нововведению появилась возможность более подробной и точной трактовки отрицательных чисел.
Декарт изучал как вещественные, так и комплексные числа. Для последних он ввёл понятие «мнимые отрицательные корни», сопрягаемые с комплексными числами.
Труды, исследования, нововведения Декарта впоследствии использовались учёными всего мира для будущих открытий.

Дирихле́, Пе́тер Гу́став Лежён
(нем. Johann Peter Gustav Lejeune Dirichlet)
Родился 13 февраля 1805 года — умер 5 мая 1859 года
Немецкий математик Дирихле работал в области теории чисел, теории функций и в области математического анализа.
С ранних лет Дирихле был увлечён математикой, поэтому родители, видя такую любовь сына, позволили получить математическое образование, определив его в гимназию в Боне, а потом в гимназию в Кёльне, где его учителем был Георг Ом[1]. После чего получал образование во Франции.
Петер Дирихле начал свои исследования будучи ещё студентом. Так, во времена учёбы он доказал «Великую теорему Ферма»[2]; для частного случая, благодаря этой работе он стал известен в кругах математиков как подающий надежду учёный.
После учёбы Дирихле начал работать преподавателем в университете, параллельно занимался исследованиями. В области теории чисел Дирихле принадлежат открытия нескольких принципов и теорем, позже получивших имя учёного, а также он разработал ядро Дирихле, скрытое распределение Дирихле. Являясь создателем аналитической теории чисел, ввёл характеры Дирихле и L-функции, доказал теорему Дирихле о единице — фундаментальный результат алгебраической теории чисел.
Теорема Дирихле.
Каждая бесконечная арифметическая прогрессия, первый член и разность которой — натуральные взаимно простые числа, содержит бесконечное число простых чисел.
В математическом анализе в 1829 году математик ввёл функцию, которую в настоящее время называют функцией Дирихле. Эта функция определена для всех действительных чисел и принимает значение 1, если её аргумент — это рациональное число, и значение 0, если её аргумент — иррациональное число (рис. 1).
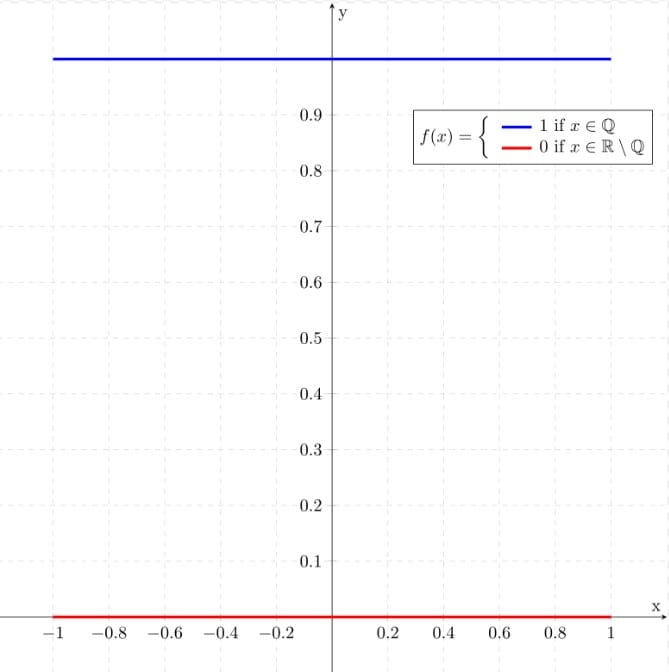
Дирихле был признанным математиком и учёным своего времени, членом Петербургской, Берлинской и Парижской академий наук, членом Лондонского королевского общества.
1 Георг Ом — немецкий физик (1787 − 1854).
2 Великая теорема Ферма — для любого натурального числа n > 2 уравнение an + bn = cn не имеет решений в целых ненулевых числах.

Евкли́д
(Эвкли́д, др.-греч. Εὐκλείδης, от «добрая слава»)
Родился примерно в 325 году до нашей эры — умер примерно в 265 году до нашей эры
Древнегреческий математик, геометр, автор самого древнего из дошедших до нас трудов по математике, в частности, по геометрии. Евклида называют первым математиком Александрийской школы III века до нашей эры. Достоверной информации о жизни Евклида очень мало. Известно только, что его научная деятельность проходила в Алек-сандрии.
Изучение естественных наук Евклид начал дома, получая знания о мире от отца, затем продолжил обучение в школе Платона. Там были заложены основы математических знаний. Позже, в Мусейоне, Платон открыл школу с лучшими математиками.
Главным трудом Евклида является его сочинение «Начала». Эта работа состоит из 13 томов, в которых были систематизированы и подробно описаны основные понятия и утверждения геометрии. Авторами этих понятий и утверждений были предшественники Евклида — Фалес, Пифагор, Аристотель, Евдокс и другие. Каждый том «Начал» посвящён отдельным темам, таким как свойства параллелограммов и треугольников, принципы и закономерности геометрической алгебры, геометрия окружностей, вписанных и описанных многоугольников, общая теория пропорции и её применение к теории подобия фигур, теория чисел, классификация иррациональностей, основы стереометрии, правила нахождения объёмов конусов и пирамид, площади круга, правила построения пяти правильных многогранников («платоновых тел»).
Евклида называют отцом геометрии. Его труд «Начала» почти 2000 лет являлся главной книгой, по которой изучали геометрию. В своей работе он сформулировал 5 постулатов[1] — основ всей геометрии:
- Из каждой точки к каждой точке можно провести прямую и притом только одну.
- Отрезок можно непрерывно продолжить до прямой.
- Из любого центра любым радиусом можно описать окружность.
- Все прямые углы равны друг другу.
- Если прямая пересекает две прямые и образует внутренние односторонние углы в сумме меньше двух прямых, то при неограниченном продолжении этих двух прямых они пересекутся с той стороны, где сумма углов меньше двух прямых.
Евклид
1 Нобелевская премия — наиболее престижная международная премия в области науки, литературы и общественной деятельности.

Ка́нтор, Георг
(нем. Georg Ferdinand Ludwig Philipp Cantor)
Родился 3 марта 1845 года — умер 6 января 1918 года
Немецкий математик родился в Санкт-Петербурге, где жили многие родственники его отца. Но в 1856 году семья переехала в Германию.
Ещё с раннего возраста имел математические способности. Блестяще окончил училище с математической направленностью. После обучения в университете получил степень доктора за работу в области теории чисел. Далее стал преподавателем, ведя параллельно научную деятельность.
В своих исследованиях Кантор определяет вещественное число как класс фундаментальных последовательностей рациональных чисел. Канторовская модель была чисто математической, без обращения к геометрии, в отличие от общепринятой тогда модели.
Кантор занимался теорией множеств. Ввёл понятие мощности множества, показал, что рациональных чисел столько же сколько натуральных, а вещественных гораздо больше. Работая в области теории множеств, Георг Кантор показал, что множества точек отрезка и точек квадрата имеют одну и туже мощность, независимо от длинны отрезка и ширины квадрата. Мнения о работе Кантора разделились. Часть ведущих математиков того времени критиковали её, другая часть — одобряла. Одни называли Георга «научным шарлатаном», другие же «математическим гением».
Наиболее значимый труд Кантора — это «Основы общего учения о многообразиях». Позже многообразия он стал называть множествами.
Несмотря на огромную критику Канторовская теория множеств в дальнейшем получила развитие и стала применяться для решения различных научных проблем.
Именем Кантора назван кратер на обратной стороне Луны.

Карда́но, Джеро́ламо (Джироламо, Иероним)
(лат. Hieronymus Cardanus, итал. Girolamo Cardano, Gerolamo Cardano)
Родился 24 сентября 1501 года — умер 21 сентября 1576 года
Итальянский математик, инженер, философ, врач, астролог родился в Павии (Италия). Обучение начал в 1520 году в университете в Павии, а продолжил — в университете в Падуи. Сначала он занимался только медициной, но к 1534 году стал проявлять активный интерес к математике — он был профессором математики сначала в Милане, а позже в Болонье, не оставляя при этом медицину.
Джероламо Кардано опубликовал достаточно много работ, среди которых — фундаментальные труды по алгебре, теории вероятностей.
Решая задачу нахождения корней кубического уравнения y3 + py + q = 0, которое можно получить из уравнения ax3 + bx2 + cx + d = 0, Кардано получил формулу
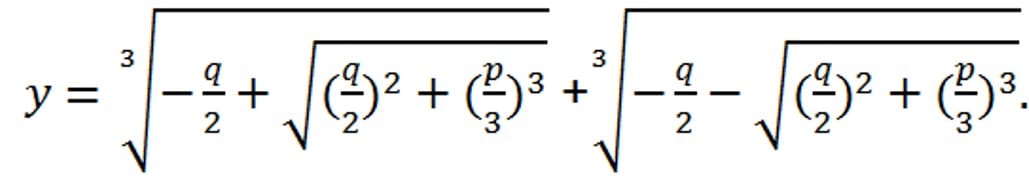
В настоящее время эта формула носит имя этого итальянского учёного, хотя он сам признавался, что узнал её от другого учёного — Никколо Тартальи. Об этом, как и о других открытиях, сделанных совместно с учеником Лодовико (Луиджи) Феррари, Джероламо Кардано писал в своём труде «Великое искусство». Одним из таких открытий является метод Феррари решения уравнений четвёртой степени.
Хотя большого прикладного значения формулы не получили, методы, использованные Кардано, стали основой для введения нового для того времени объекта — комплексных чисел.
Кроме того, Кардано одним из первых в Европе стал рассматривать отрицательные корни уравнений.
В 1663 году, уже после смерти Кардано, была издана его работа «Книга об игре в кости». В этой работе Д. Кардано исследовал математическую теорию азартных игр. Это был один из первых трудов по комбинаторике и теории вероятностей. Не смотря на некоторые ошибки, Кардано достаточно близко подошёл к общему понятию вероятности, практически предсказал «закон больших чисел».
Джероламо Кардано вписал своё имя и в историю криптографии — он изобрёл шифровальное устройство, которое использовали в переписках. Это устройство носит имя «решётка Кардано». Позднее эту форму стеганографии[1] преобразовали в шифр «Поворотная решётка».
Помимо математики и теории вероятностей, Кардано публиковал работы по медицине, астрономии, механике.
1 Стеганография — способ передачи или хранения информации с учётом сохранения в тайне самого факта такой передачи (хранения).

Клейн, Фе́ликс Христиа́н
(нем. Felix Christian Klein)
Родился 25 апреля 1849 года — умер 22 июня 1925 года
Немецкий математик, педагог родился в Дюссельдорфе (Пруссия) в семье чиновника. После гимназии изучал математику и физику в Боннском университете. В 1868 году стал доктором.
В 1872 году Феликс Клейн становится профессором Эрлангенского университета. После Эрлангенского университета Клейн преподавал в Высшей технической школе Мюнхена, в университете Лейпцига, в Гёттингенском университете.
В 1872 году молодой учёный опубликовал доклад «Сравнительное обозрение новейших геометрических исследований», вошедший в историю науки как «Эрлангенская программа». В ней он предложил использовать алгебраическую классификацию различных областей геометрии так, чтобы разным разделам соответствовали разные группы преобразований пространства, а объектами изучения были инварианты[1] этих преобразований.
Феликс Клейн первым доказал, что геометрия Лобачевского — пространство постоянной отрицательной кривизны[2].
В 1882 году Клейн привёл пример односторонней замкнутой поверхности, которая не имеет краёв. Он взял мысленно цилиндр, воткнул один его край в бок и соединил со вторым краем. Так он получил бутылку Клейна (рис. 1). В трёхмерном пространстве отверстие в боку цилиндра необходимо, а вот в четырёхмерном пространстве отверстие уже не понадобится.
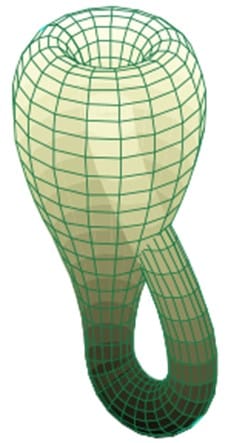

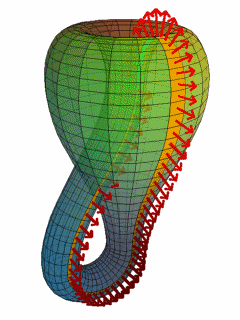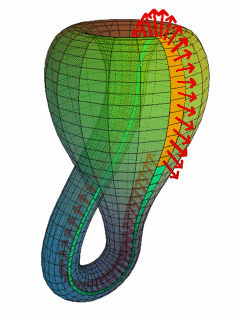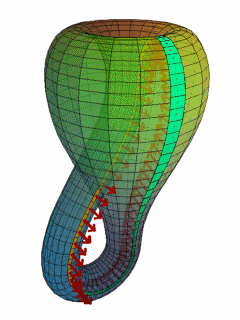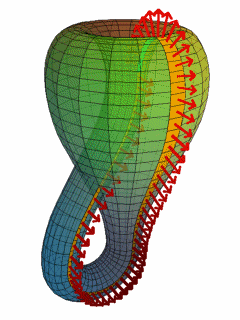
Кроме этого, Феликс Клейн публиковал работы о решении уравнений пятой, шестой, седьмой степени, об интегрировании дифференциальных уравнений, об абелевых функциях, о неэвклидовой геометрии.
Также Клейн принимал участие в издании трудов Карла Фридриха Гаусса, первой Математической энциклопедии, в реформе школьного образования.
1 Инвариант — свойство объекта, которое не изменяется при определённых преобразованиях.
2 Кривизна — характеристика, которая описывает отклонение заданного геометрического объекта от соответствующего ему «плоского» объекта.

Ковале́вская, Со́фья Васи́льевна
(урождённая Корвин-Круковская)
Родилась 15 января 1850 года — умерла 10 февраля 1891 года
Первая в мире женщина — профессор математики, русский учёный, математик, механик — родилась в Москве в семье генерал-лейтенанта артиллерии. Образование получала домашнее. Но продолжить образование в университетах женщинам было в то время невозможно. Для того, чтобы учиться в университетах Европы, Софья Вышла замуж и с 1869 году поступила в Гейдельбергский университет, посещая лекции Густава Кирхгофа и других видных учёных, а с 1870 по 1874 год обучалась лично у Карла Вейерштрасса, поскольку в Берлинском университете женщины обучаться не могли.
В 1874 году Софья Ковалевская защитила диссертацию, связанную с решением задач теории дифференциальных уравнений в частных производных, и Гёттингенский университет присвоил ей степень доктора философии по математике и магистра изящных искусств.
По возвращении в Петербург Софья преподавала математику в женской гимназии и долгое время не возвращалась в науку. В 1883 году Ковалевская уезжает из России и, благодаря помощи и содействию Карла Вейерштрасса, получила возможность преподавать в Стокгольмском университете, а в 1889 году получила там звание профессора.
Основными научными интересами Софьи были:
— вопросы теории вращения твёрдых тел, математическая физика. Ковалевская открыла третий классический случай разрешимости задачи о вращении твёрдого тела вокруг неподвижной точки. В этом направлении она продолжила решение задачи, которое начал Леонард Эйлер и Жозеф Луи Лагранж. Также занималась исследованием вращения тяжёлого несимметричного волчка;
— дифференциальные уравнения в частных производных, теория потенциалов. Ковалевская доказала, что задача Коши для систем дифференциальных уравнений в частных производных существует аналитическое решение;
— астрономия, небесная механика. Софья исследовала задачу Лапласа о равновесии кольца Сатурна и получила второе приближение;
— интегральное исчисление. Ковалевская решила задачу о приведении некоторого класса абелевых интегралов третьего ранга к эллиптическим интегралам.
За свои научные достижения Софья Ковалевская была удостоена таких наград, как премия Бордена Парижской академии наук, премия Шведской академии наук. Её именем назван кратер на Луне.
Женщины в русской истории — Софья Васильевна Ковалевская

Колмого́ров, Андре́й Никола́евич
Родился 25 апреля 1903 года — умер 20 октября 1987 года
Советский математик, один из крупнейших математиков XX века родился в Тамбове, рос и воспитывался в Ярославле в семье своей тёти Веры Колмогоровой. В 1910 году был определён в частную гимназию в Москве, где начал показывать свои математические способности.
В 1920 году Андрей Колмогоров поступил сразу на два математических отделения — Московского университета и Химико-технологического института имени Д. И. Менделеева, чтобы учиться у лучших педагогов того времени. Во время учёбы он ещё и работал школьным учителем.
В 1922 году были опубликованы работы Колмогорова о рядах Фурье[1], где привёл пример ряда, который расходится почти всюду, и ряда, который расходится в каждой точке. Это принесло студенту мировую известность.
Дальнейшей областью исследований Колмогорова стала теория вероятностей. Здесь учёный предложил свою систему аксиом, на базе которой появилась возможность построить математическую теорию, которая применима на практике. Совместно с Алексанром Яковлевичем Хинчиным Андрей Николаевич внёс огромный вклад в развитие теории вероятностей и математической статистики. В 1928 году он определил и доказал условия закона больших чисел.
В 1931 году А. Н. Колмогоров стал профессором МГУ, а в 1935 году ему была присвоена степень доктора физико-математических наук без защиты диссертации. До конца жизни Колмогоров работал в МГУ как декан механико-математического факультета, заведующий кафедрой теории вероятностей, Межфакультетской лабораторией вероятностных и статистических методов, кафедрой математической логики.
Помимо исследований по теории вероятностей, теории случайных процессов, Андрей Николаевич работал в таких областях, как турбулентность, теория сложности в алгоритмической области математики и информатики, небесная механика, динамические системы, теория функций действительного аргумента.
Большой вклад Колмогоров внёс в изменение подхода к изучению математики. Благодаря его работам, появились новые учебники по алгебре и геометрии, по которым учились много лет. Также учёный принимал участие в подготовке математического раздела Большой Советской Энциклопедии.
Андрей Колмогоров
1 Ряд Фурье — это представление периодической функции в виде ряда 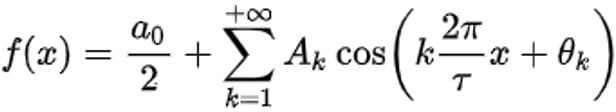 .
.
Коши́, Огюсте́н Луи́, барон
(фр. Augustin Louis Cauchy)
Родился 21 августа 1789 года — умер 23 мая 1857 года
Великий французский математик и механик родился в Париже в семье высокопоставленного чиновника. Огюстен учился в Политехнической школе, в парижской Школе мостов и дорог, затем работал инженером путей сообщения в городе Шербург и занимался математическими исследованиями.
После возвращения в Париж Коши в 1815 году получает место в Политехнической школе, а позже становится профессором школы. В 1816 году королевским указом Коши был назначен членом Парижской академии, а в 1848 году получил место в Сорбонне.
За свою жизнь Огюстен Луи Коши написал более 800 работ в различных областях математики и механики. Основные его труды относятся к математическому анализу. В этой области математики учёный дал строгие определения таким базовым понятиям, как предел, непрерывность, производная, дифференциал, интеграл, сходимость ряда, радиус сходимости ряда.
Определения понятий математического анализа Коши давал на языке бесконечно малых, понимая под бесконечно малой переменную величину, которая стремится к нулю.
Определение предела функции по Коши.
Число b называется пределом функции y = f(x) в точке a, если для каждого малого положительного числа ε > 0 существует малое положительное число δ = δ(ε) > 0, что для всех значений x, удовлетворяющих условию 0 < |x − a| < δ выполняется неравенство |f(x) − b| < ε.
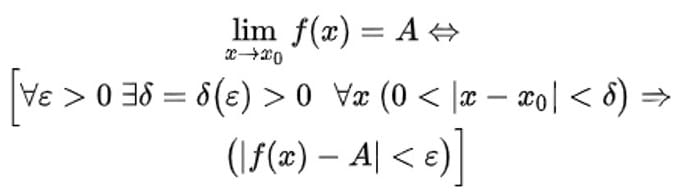
Коши развил основы теории функции комплексного переменного, заложенные Леонардом Эйлером и Жаном Лероном Д’Аламбером, введя понятия «модуль комплексного числа», «сопряжённые комплексные числа», доказал теорему Тейлора, для которой вычислил остаточный член. В области теории дифференциальных уравнений Коши сформулировал одну из наиболее важных общих задач (задач Коши), основные теоремы существования решений, метод решения уравнений первого порядка с частными производными.
Кроме математического анализа, Огюсту Коши принадлежат работы по теории многогранников, теории симметрических многочленов, теории определителей.
Также Коши проводил исследования в области механики сплошных сред, оптике, волновой теории света, астрономии и других областях естествознания.
Фильм о Великом французском математике Коши