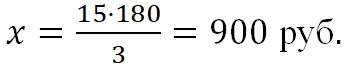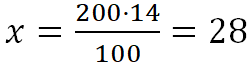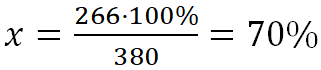ТЕКСТ ДЛЯ ЧТЕНИЯ

1. Понятие десятичной дроби 

Дроби 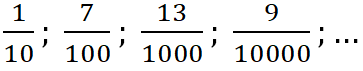 можно записать так: 

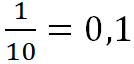(нуль целых, одна десятая), 

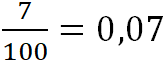(нуль целых, семь сотых), 

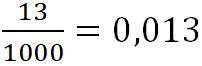(нуль целых, тринадцать тысячных), 

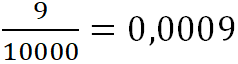(нуль целых, девять десятитысячных). 

Числа 0,1; 0,07; 0,013; 0,0009; ... – это десятичные дроби. 

Запомните, как читать десятичные дроби!

Десятичные дроби имеют две части: целую и дробную. 

Дробь 13,056 – это десятичная дробь, у которой 13 – это целая часть, а 056 – это дробная часть. Целая часть и дробная часть числа 13,056 отделяются запятой. Дробная часть имеет три цифры – 0, 5 и 6. Это значит, что десятичная дробь 13,056 имеет знаменатель 1000: 

 

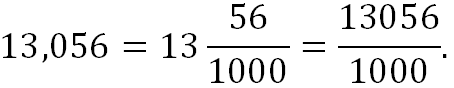
2. Свойства десятичной дроби 

1. К любой десятичной дроби можно приписать нули справа (в дробной части), при этом получится дробь, равная данной: 

0,8 = 0,80 = 0,800 = 0,8000 = ... 

2. Если в десятичной дроби нули записаны справа (в дробной части), то их можно отбросить, при этом получится дробь, равная данной. 

3. Если в десятичной дроби приписать нули слева (в целой части), то величина дроби не изменится: 

0,12 = 00,12 = 000,12 = 0000,12 = ... 

 

3. Действия с десятичными дробями 

Сложение и вычитание десятичных дробей выполняются так же, как сложение и вычитание обыкновенных дробей. Сначала надо привести дроби к общему знаменателю, а затем выполнить действие. 

Привести десятичные дроби к общему знаменателю – значит уравнять число знаков после запятой (в дробной части). 

Например, выполним действия 0,2 + 0,05 – 0,023: 

0,2 + 0,05 – 0,023 = 0,200 + 0,050 – 0,023 = 0,227. 

Чтобы перемножить две десятичные дроби, надо: 

1) убрать запятую; 

2) перемножить новые числа; 

3) в полученном произведении справа отделить запятой столько цифр, сколько их было после запятых во всех множителях вместе. 

Например, 

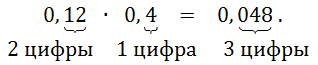
Чтобы разделить десятичную дробь на целое число, надо сначала разделить целую часть на это число, поставить запятую, а затем разделить дробную часть на это число. 

Чтобы разделить десятичную дробь на десятичную дробь, надо сначала перенести запятую у делимого и делителя вправо на столько цифр, сколько их у делителя в дробной части. Затем выполнить деление на целое число. 

 

4. Конечные и бесконечные десятичные дроби 

Десятичные дроби бывают конечные и бесконечные. В конечной десятичной дроби после запятой стоит конечное число цифр. В бесконечной десятичной дроби после запятой стоит бесконечно много цифр. 

Пример. 1,1; 7,03; 0,004 – это конечные дроби; 

0,171717...; 0,10110111011110... – это бесконечные дроби. 

Если конечную десятичную дробь записать в виде обыкновенной несократимой дроби , то её знаменатель q не имеет других простых делителей, кроме чисел 2 и 5. 

Например,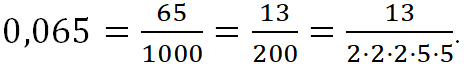  

Верно и обратное. Если знаменатель q несократимой дроби не имеет других простых делителей, кроме чисел 2 и 5, то эту дробь можно записать как конечную десятичную дробь. 

Например,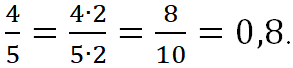  

Если знаменатель q несократимой дроби  имеет простой делитель, неравный числам 2 и 5, то эту дробь нельзя записать как конечную десятичную дробь. 

Например, 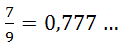. Это бесконечная периодическая дробь. . Цифра 7 – это период дроби. Эта цифра повторяется в записи дроби бесконечное число раз. 

Читаем периодические дроби так: 

– «нуль целых и семь в периоде»; 

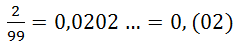– «нуль целых и нуль два в периоде»; 

– «три целых, одна десятая и семь в периоде». 

К любому числу или конечной десятичной дроби можно справа приписать бесконечно много нулей. Это значит, что любое число или конечную десятичную дробь можно записать как бесконечную периодическую дробь с периодом нуль. 

Пример. 1 = 1,000000... = 1,(0); 4,6 = 4,6000000... = 4,6(0). 

Не все бесконечные дроби можно записать в виде обыкновенной дроби. Такие числа, как 0,01001000100001..., p = 3,141592653589793..., e = 2,71828182845904..., 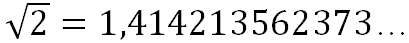– это бесконечные непериодические десятичные дроби. 

Бесконечные дроби (периодические и непериодические) можно округлять – записывать только часть знаков после запятой, а остальные знаки отбрасывать. Чтобы округлить число, используют правила: 

1) если при округлении чисел первая из цифр, которые отбрасывают, меньше, чем 5 (0, 1, 2, 3, 4), то последняя из цифр, которые оставляют, остаётся без изменений; 

2) если при округлении чисел первая из цифр, которые отбрасывают, больше или равна 5 (5, 6, 7, 8, 9), то последняя из цифр, которые оставляют, увеличивается на 1. 

Пример. Запишем обыкновенные дроби 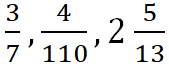 как десятичные, результат округлим до тысячных, то есть оставим три знака после запятой: 

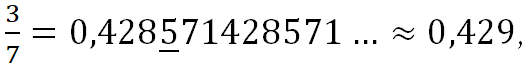так как первая цифра, которую надо отбросить, – это 5 ≥ 5; 

так как первая цифра, которую надо отбросить, – это 3 < 5; 

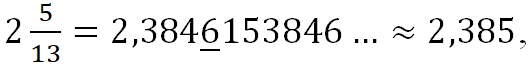так как первая цифра, которую надо отбросить, – это 6 ≥ 5. 

 

5. Действия с обыкновенными и десятичными дробями 

Чтобы выполнить действия с обыкновенными и десятичными дробями, нужно все числа записать как обыкновенные дроби или все числа записать как конечные десятичные дроби и выполнить действия. 

Пример. Найдём значение выражения .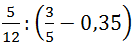 

1.  Сначала выполним вычитание, используя десятичные дроби: 

.

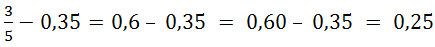2.  Затем выполним деление, используя обыкновенные дроби: 

 

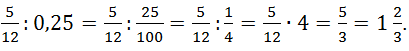
Таким образом, мы нашли точное значение выражения. 

 

6. Отношение. Пропорция 

Частное двух чисел a и b, которые не равны нулю, – это отношение a к b. Числа a и b – это члены отношения. Например, 5 : 2 или  – это отношение числа 5 к числу 2 (отношение пяти к двум). 

Отношение чисел 2 и 5 не равно отношению 5 и 2, потому что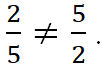  

Равенство двух отношений – это пропорция.  Пропорция имеет вид:

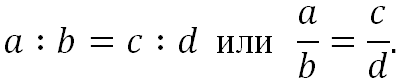
Числа a и d – это крайние члены пропорции. Числа b и c – это средние члены пропорции. 

Пример. 7 : 14 = 4 : 8 – это пропорция. Здесь 7 и 8 – это крайние члены пропорции, а 14 и 4 – это средние члены. Читаем так: «отношение чисел 7 и 14 равно отношению чисел 4 и 8» или «7 относится к числу 14 как 4 относится к числу 8». 

Запомните, как читать пропорции!

Из пропорции 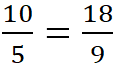 следует пропорция 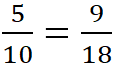, потому что если дроби равны, то и обратные им дроби равны. 

Основное свойство пропорции. 

Произведение крайних членов пропорции равно произведению средних членов пропорции: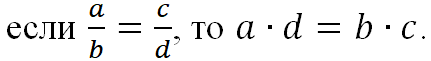  

Пример. Рассмотрим пропорцию 9 : 3 = 15 : 5. По свойству пропорции 9 · 5 = 3 · 15 = 45. 

Если один из членов пропорции неизвестен и необходимо его найти, то говорят, что нужно решить пропорцию. 

Пример. За 3 кг сахара заплатили 180 рублей. Сколько нужно заплатить за 15 кг сахара? 

Составим пропорцию 

 

7. Проценты 

Сотая часть числа – это процент. Обозначается процент знаком %. 

Запомните, как читать проценты!

Если число принять за 1, то 1% составляет 0,01 этого числа. 50% составляют 0,5 этого числа и так далее. 

Пример. 

1. Найти 14% от числа 200. 

Составим пропорцию 

2. В книге 380 страниц. Девочка прочитала 266 страниц. Сколько процентов всей книги она прочитала? 

Составим пропорцию