(сущ., ср.р., р.п. равенства)

Формула, которая состоит из двух выражений, соединённых знаком «=». Виды: верное, неверное, числовое, с переменными. 

Пример. Запишите числовое равенство 12 + 45 • 61 = 3990 – 127 • 12.

Знак равенства. 

Пример. 21 + 34 = 10 + 45.

(сущ., ж.р., р.п. равносильности)

Свойство двух или нескольких уравнений с одним неизвестным (или систем n уравнений с n неизвестными), которое заключается в том, что они имеют одно и то же множество корней (решений). 

Пример. Проверьте равносильность уравнений 2x + 7 = 25 и 63 – 6x = 15.

прил. равносильный, -ая, -ое, -ые.

(сущ., м.р., р.п. радикала)

Математический знак «√», который обозначает операцию извлечения корня, ставится перед числом или выражением, из которого извлекается корень. 

Пример. Уединение радикала – один из методов решения иррациональных уравнений.

(сущ., м.р., р.п. раздела)

1. Часть какого-нибудь текста. 

2. Специальная область какой-нибудь науки. 

Пример. Арифметика – это раздел математики.

гл. разделять, разделить.

(гл., сов., разделить что? на что?)

1. Выполнить действие деления. 

2. Из целого сделать части. 

3. Знак действия деления. 

Пример. 1. 120 разделить на 10 будет 12.

   2. 120 : 10 = 12, 176 ÷ 11 = 16, 72 / 8 = 9.

(ср.р., р.п. разложения многочлена на множители)

1. Запись многочлена как произведения нескольких многочленов. 

2. Тождественное преобразование алгебраического выражения в произведение нескольких множителей. 

Пример. Разложите многочлен a⁴ + 4 на множители методом введения вспомогательных членов.

(ср.р., р.п. разложения числа на простые множители)

Запись составного числа в виде произведения всех его простых делителей или их степеней. 

Пример. Разложите число 47 256 на простые множители.

(сущ., ж.р., р.п. разности)

1. Результат действия вычитания, то есть такое число с = a – b, что его сумма с числом bравна числу a. 

2. Выражение a – b. 

Пример. Для целых чисел всегда можно найти их разность.

прил. разностный, -ая, -ое, -ые.

(ср.р., р.п. раскрытия скобок)

Переход от записи a(b + c) к записи ab + ac. 

Пример. Чтобы выполнить раскрытие скобок, используют дистрибутивный закон умножения.

(ср.р., р.п. рационального выражения)

Алгебраическое выражение с переменной, в котором используются только арифметические действия. Виды: целое рациональное выражение (одночлен, многочлен), дробно-рациональное выражение (алгебраическая дробь). 

Пример. Назовите виды рациональных выражений и приведите примеры.

(ср.р., р.п. рационального уравнения)

Уравнение вида f(x) = 0, где f(x) – рациональное выражение. 

Пример. Назовите методы решения рациональных уравнений.

(ср.р., р.п. рационального числа)

Число, которое можно записать в виде , где p, q – целые числа и q ≠ 0. Все рациональные числа образуют множество рациональных чисел Q. 

Пример. Рациональное число  – это положительная дробь, если p, q имеют одинаковый знак.

(сущ., ср.р., р.п. решения)

1. Математический объект, который удовлетворяет условиям поставленной задачи. 

2. Процесс поиска решения. 

3. Выбор одной из нескольких возможностей, которые удовлетворяют заданным условиям. 

Пример. 1. Запишите решение неравенства 2x² + 5x – 10 > 0.

   2. Множество решений системы двух уравнений с двумя неизвестными – это упорядоченная пара чисел.

(гл., сов.) решить II (что?) пропорцию, несов. решать I (что?)

Найти неизвестный член пропорции. 

Пример. Решить пропорцию .

(м.р., р.п. ряда натуральных чисел)

Упорядоченная последовательность всех натуральных чисел. 

Пример. Все натуральные числа 1, 2, 3, 4, … образуют ряд натуральных чисел.

(ср.р., р.п. ряда целых чисел)

Упорядоченная последовательность всех целых чисел. 

Пример. Натуральные числа, им противоположные числа и нуль образуют ряд целых чисел.

(м.р., р.п. свободного члена)

Член многочлена, который не содержит переменной величины. 

Пример. Свободный член квадратного трёхчлена ax² + bx + с – это число c.

(сущ., ср.р., р.п. свойства)

Характеристика объекта, понятия, действия. 

Пример. Назовите основное свойство дроби.

(ср.р., р.п. свойства обыкновенной дроби)

Если числитель и знаменатель дроби умножить на одно и то же натуральное число, то получится дробь, которая равна данной дроби: . 

Пример. Свойство обыкновенной дроби используют, чтобы сократить дробь и привести дробь к новому знаменателю.

(ср.р., р.п. свойства пропо рции)

Произведение крайних членов пропорции равно произведению средних членов пропорции: если , то . 

Пример. Свойство пропорции используют, чтобы решить пропорцию.

(ср.р., р.п. свойства частного чисел)

Делимое и делитель можно умножить или разделить на одно и то же натуральное число – частное от этого не изменится. 

Пример. Свойство частного чисел используют, чтобы упростить вычисления.

(сущ., м.р., р.п. синуса)

1. Тригонометрическая функция y = sin x. 

2. Ордината конца подвижного единичного радиус-вектора. 

Пример. Найдите sin 45°.

(сущ., ж.р., р.п. синусоиды)

Кривая линия, график функции y = sin x. 

Пример. Изобразите на чертеже синусоиду.

(ж.р., р.п. системы координат)

1. Совокупность условий, которые определяют положение точки на прямой, на плоскости, в пространстве. 

2. Совокупность выделенных точек, линий и поверхностей, с помощью которых определяется положение геометрических объектов. 

Пример. Изобразите на плоскости декартову систему координат.

(ж.р., р.п. системы уравнений)

Множество уравнений с n неизвестными, для которых требуется найти значения неизвестных, удовлетворяющих одновременно всем уравнениям системы. 

Пример. Система двух линейных уравнений с двумя неизвестными имеет вид

(сущ., ср.р., р.п. решения)

Величина, каждое значение которой может быть выражено одним действительным числом, без учёта направления или другой какой-либо оценки. 

Пример. В записи  величина λ – это скаляр, а   – вектор.

прил. скалярный, -ая, -ое, -ые

(ср.р., р.п. скалярного произведения векторов)

Число, которое можно найти по формуле , где a₁, a₂ – координаты вектора  , b₁, b₂ – координаты вектора . 

Пример. Найдите скалярное произведение векторов  и .

(сущ., мн., р.п. скобок, ед. скобка)

Математические знаки (), [], {}, которые употребляют парами для выделения какой-либо части математической формулы, для обозначения порядка действий или для обозначения различных понятий. Виды: круглые, квадратные, фигурные и другие. 

Пример. Заключите выражение в скобки.

(мн., р.п. скрещивающихся прямых)

Прямые в пространстве, которые не лежат в одной плоскости. 

Пример. Покажите на чертеже скрещивающиеся прямые.

(сущ., ср.р., р.п. слагаемого)

1. Любой из элементов, над которым производится операция сложения. 

2. Компонента действия сложения. 

Пример. В записи a + b = c величины a и b – это слагаемые.

(сущ., ср.р., р.п. сложения)

Арифметическое действие. Знак действия сложения – плюс, компоненты – слагаемые, результат – сумма. 

Пример. 1. Формула сложения: a + b= c.

2. Выполните сложение заданных чисел.

(ж.р., р.п. смешанной дроби)

Число, которое состоит из целой и дробной частей; сумма целого числа и правильной дроби. 

Пример. 1. Числа  – это смешанные дроби.

   2. Смешанную дробь можно записать как неправильную.

(мн., р.п. совпадающих прямых)

Прямые, у которых все точки общие. 

Пример. Найдите на чертеже совпадающие прямые.

(ж.р., р.п. сократимой дроби)

Дробь, у которой числитель и знаменатель имеют общий множитель, который не равен единице. 

Пример. Числа  – сократимые дроби.

(сущ., ср.р., р.п. сокращения)

Тождественное преобразование дроби, которое выполняется с помощью основного свойства дроби. Чтобы сократить дробь, нужно числитель и знаменатель данной дроби разделить на их общий множитель, отличный от нуля и единицы. 

Пример. Выполните сокращение дробей .

гл. сокращать, сократить

(мн., р.п. сопряжённых выражений)

Выражения вида a + b и a – b. 

Пример. Выражения  и  – это сопряжённые выражения.

(мн., р.п. сопряжённых чисел)

Комплексные числа вида a + bi и a – bi. 

Пример. Числа 5 + 7i и 5 – 7i – это сопряжённые числа.

(ср.р., р.п. составного числа)

Натуральное число, которое больше единицы и делится на 1, на себя и ещё хотя бы на одно натуральное число. 

Пример. 1. Числа 12, 56, 100 – это составные числа.

   2. Составное число имеет больше двух делителей.

(сущ., м.р., р.п. способа)

Выбор последовательности действий при решении математических задач. 

Пример. В произведении нескольких множителей можно переставлять множители и заключать их в скобки любым способом.

(ср.р., р.п. сравнения чисел)

Действие с числами, результатом которого является одно из соотношений a > b, a < b, a = b. 

Пример. Выполните сравнение заданных чисел.

гл. сравнивать, сравнить.

(м.р., р.п. среднего члена пропорции)

Величины b и c в пропорции а : b = c : d. 

Пример. Назовите средние члены в пропорции .

(сущ., ср.р., р.п. решения)

Член многочлена, который имеет наибольшую степень. 

Пример. В выражении 3x² + 4x – 5x⁴ + 2 одночлен (–5x⁴) – это старший член многочлена.

(ж.р., р.п. степенной функции)

Функция, которая задана формулой  (x > 0), где  – постоянное число. 

Пример. Свойства и графики степенной функции  зависят от показателя степени a.

(сущ., ж.р., р.п. степени)

1. Результат действия возведения в степень. 

2. Выражение aⁿ. 

Пример. В записи aⁿ = b выражение aⁿ – это степень.

прил. степенной, -ая, -ое, -ые.

(сущ., ж.р., р.п. степени многочлена)

Наибольшая степень одночлена, входящего в данный многочлен. 

Пример. Степень многочлена 3x² + 4x – 5x⁴ + 2 равна числу 4.

(сущ., ж.р., р.п. степени одночлена)

Сумма показателей степеней всех переменных, которые входят в данный одночлен. 

Пример. Степень одночлена 3x²yz⁴ равна числу 7.

(ж.р., р.п. степени с дробным показателем)

Выражение . Значение этого выражения можно найти по формуле . 

Пример. Назовите свойства степени с дробным показателем.

(ж.р., р.п. степени с натуральным показателем)

Произведение n множителей, каждый из которых равен a:  

Пример. Назовите свойства степени с натуральным показателем.

(сущ., ср.р., р.п. решения)

Выражение a^m, где m ∈ Z. Если m > 0, то имеет место степень с натуральным показателем. Если m < 0, то значение выражения можно найти по формуле . 

Пример. Назовите свойства степени с целым показателем.

(сущ., ж.р., р.п. суммы)

1. Результат действия сложения. 

2. Выражение a + b. 

Пример. 1. В записи a + b = c величина c – это сумма.

   2. Сумма натуральных чисел – это натуральное число.

прил. суммарный, -ая, -ое, -ые.

гл. суммировать, просуммировать.

(сущ., ж.р., р.п. таблицы)

Перечень сведений, которые расположены в систематическом порядке – в ячейках на пересечении строк и столбцов. 

Пример. Заполните таблицу значений функции.

прил. табличный, -ая, -ое, -ые.

(сущ., м.р., р.п. тангенса)

1. Тригонометрическая функция y = tg x. 

2. Отношение ординаты конца подвижного единичного радиус-вектора к его абсциссе. 

Пример. Найдите tg 30°.

(сущ., ж.р., р.п. тангенсоиды)

Кривая линия, график функции y = tg x. 

Пример. Изобразите на чертеже тангенсоиду.

(сущ., ж.р., р.п. теоремы)

1. Предложение, истинность которого может быть доказана. Обычная запись теоремы: A ⇒ B, где A – условие, B – заключение. 

2.  Математическое предложение, истинность которого устанавливается или опровергается при помощи доказательства.  

Пример. Докажите теорему о Пифагора.

(ж.р., р.п. теоремы Виета)

Сумма корней приведённого квадратного уравнения x² + px + q = 0 равна (–p), а произведение корней равно q. 

Пример. С помощью теоремы Виета можно находить корни квадратного уравнения без формулы, только путём подбора.

(ж.р., р.п. теоремы Пифагора)

Сумма квадратов катетов прямоугольного треугольника равна квадрату его гипотенузы: c² = a² + b². 

Пример. С помощью теоремы Пифагора можно найти катет прямоугольного треугольник, если известны его гипотенуза и второй катет.

(сущ., ср.р., р.п. тождества)

Равенство выражений с переменными, которое верно при всех допустимых значениях переменных этого равенства. 

Пример. Основное тригонометрическое тождество sin²x + cos²x = 1.

прил. тождественный, -ая, -ое, -ые

(сущ., ж.р., р.п. точки)

1. Элемент какого-либо пространства, которое рассматривается как множество. 

2. Исходный объект геометрии. 

3. Значение аргумента функции. 

Пример. 1. Отметьте на координатной плоскости точку A(4; 7).

   2. Найдите точку пересечения графиков заданных функций.

прил. точечный, -ая, -ое, -ые.

(ж.р., р.п. точки максимума)

Значение аргумента x = x₀ функции y = f (x), при котором функция имеет максимум, то есть слева от значения x = x₀ функция y = f (x) возрастает, а справа убывает. 

Пример. Найдите все точки максимума заданной функции.

(ж.р., р.п. точки минимума)

Значение аргумента x = x₀ функции y = f (x), при котором функция имеет минимум, то есть слева от значения x = x₀ функция y = f (x) убывает, а справа возрастает. 

Пример. Найдите все точки максимума заданной функции.

(ср.р., р.п. точного значения)

Значение выражения, которое записано либо в виде целого числа, либо обыкновенной дроби, либо конечной десятичной дроби. 

Пример. Найдите точное значение выражения .

(сущ., ж.р., р.п. транзитивности)

Свойство бинарного отношения R, которое заключается в том, что из aRb и bRc следует aRc. Примеры транзитивных бинарных отношений: =, >, ≥, <, ≤. 

Пример. Приведите пример транзитивности неравенств.

прил. транзитивный, -ая, -ое, -ые.

(сущ., м.р., р.п. трёхчлена)

Многочлен с тремя членами. 

Пример. Рассмотрим квадратный трёхчлен.

(ср.р., р.п. тригонометрической функции)

Одна из основных элементарных функций. К тригонометрическим функциям относят следующие: синус y = sin x, косинус y = cos x, тангенс y = tg x, котангенс y = ctg x, секанс y = sec x, косеканс y = cosec x. 

Пример. Назовите основные тригонометрические функции.

(ср.р., р.п. тригонометрического выражения)

Выражение с переменными, в котором переменные являются аргументами тригонометрических функций. 

Пример. Упростите тригонометрическое выражение .

(ср.р., р.п. тригонометрического уравнения)

Уравнение вида f(x) = 0, где f(x) – тригонометрическое выражение. К простейшим уравнениям относятся уравнения вида sin x = a, cos x = a, tg x = a, ctg x = a. 

Пример. Назовите основные методы решения тригонометрических уравнений.

(сущ., ж.р., р.п. тригонометрии)

Раздел математики, который изучает зависимости между величинами углов и длинами сторон треугольников, свойства тригонометрических функций и связи между ними. 

Пример. Назовите основные формулы тригонометрии.

прил. тригонометрический, -ая, -ое, -ие.

(м.р., р.п. тупого угла)

Угол, величина которого больше 90°, но меньше 180°. 

Пример. Угол 145° – это тупой угол.

(ср.р., р.п. убывания функции)

Свойство функции, при котором большему значению аргумента соответствует меньшее значение функции. 

Пример. Определите промежутки убывания функции y = cos x.

гл. убывать.

(ж.р., р.п. убывающей функции)

Такая функция y = f (x), у которой для любых x₁, x₂ ∈ (a, b) при x₁ < x₂ верно неравенство f (x₁) > f (x₂). 

Пример. Функция y = x² при x < 0 убывает.

(сущ., м.р., р.п. угла)

1. Геометрическая фигура, которая образована двумя лучами, выходящими из одной точки. 

2. Мера наклона между двумя прямыми линиями или плоскостями. 

3. Мера поворота луча вокруг его начала. 

Виды: прямой, острый, тупой, развёрнутый, внутренний, внешний и другие. 

Пример. Определите угол между прямыми a и b.

прил. угловой, -ая, -ое, -ые.

(м.р., р.п. угла между векторами)

Угол между равными им векторами с общим началом. Угол между одинаково направленными векторами считается равным нулю. 

Пример. Определите угол между векторами  и .

(сущ., ср.р., р.п. уменьшаемого)

Первая компонента вычитания, то число, из которого вычитается другое число. 

Пример. В записи a – b = c величина a – это уменьшаемое.

(сущ., ср.р., р.п. умножения)

Арифметическое действие. Знак действия умножения – умножить «•» и косой крест «×», компоненты – множители, результат – произведение. 

Пример. 1. Формула умножения: a • b = c или a × b = c.

   2. Рассмотрим умножение натуральных чисел.

гл. умножать, умножить.

(гл., сов., умножить что? на что?)

1. Выполнить действие умножения. 

2. Увеличить в числе, количестве. 

3. Знак действия умножения. 

Пример. 1. 34 умножить на 2 будет 68.

   2. 34 • 2 = 68; 7 × 8 = 56.

(сущ., ж.р., р.п. тригонометрии)

Два числа (две переменных), которые имеют строго определённое местоположение, строгий порядок следования. 

Пример. Пара декартовых координат точки – это упорядоченная пара чисел.

(сущ., ср.р., р.п. уравнения)

1. Равенство, которое содержит одно или несколько неизвестных и верно только при определённых значениях этих неизвестных. 

2. Запись в форме равенства задачи о нахождении значений аргументов, при которых значения двух данных функций равны. 

Виды: алгебраическое, трансцендентное, линейное, квадратное и другие. 

Пример. Решите иррациональное уравнение .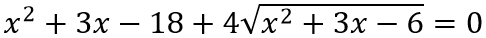

гл. уравнивать, уравнять.

(сущ., м.р., р.п. факториала)

Функция, определённая на множестве целых неотрицательных чисел, значение которой равно произведению натуральных чисел от числа 1 до данного натурального числа n.
n! = 1 • 2 • … • n. По определению 0! = 1. 

Пример. Для обозначения факториала используют запись n!.

(мн., р.п. фигурных скобок)

Знаки {}, которые используют для записи множества перечислением его элементов, для записи последовательности с указанием её общего члена, для определения порядка действий в выражении. 

Пример. Все натуральные числа можно записать как множество N = {1; 2; 3; …}.

(сущ., ж.р., р.п. формулы)

Символическая запись, которая состоит из цифр, букв, специальных знаков, расположенных в определённом порядке, и является носителем информации. 

Пример. 1. Формула корней квадратного уравнения имеет вид .

   2. Назовите формулы сокращённого умножения.

прил. формульный, -ая, -ое, -ые.

(сущ., ж.р., р.п. функции)

1. Одно из основных понятий математики, однозначное соответствие между элементами числовых множеств X и Y, которое обозначается y = f(x) (или f : X Y). Здесь x ∈ X – это аргумент, y ∈ Y – это значение функции. 

2. Зависимость значений переменной y от значений переменной x, при которой каждому допустимому значению x соответствует единственное значение y. 

Виды: основная элементарная, алгебраическая, трансцендентная, степенная, показательная, логарифмическая, тригонометрическая, обратная тригонометрическая и другие. 

Пример. Назовите основные элементарные функии.

прил. функциональный, -ая, -ое, -ые.

(ср.р., р.п. целого алгебраического выражения)

Алгебраическое выражение с переменными, которое содержит только действия сложения, вычитания, умножения и возведения в целую неотрицательную степень. 

Пример. Одночлены и многочлены – это целые алгебраические выражения.

(ср.р., р.п. целого числа)

Одно из совокупности чисел 0, ± 1, ± 2,…; элемент множества целых чисел Z. 

Пример. 4 и – 4 – это целые числа.

(сущ., ж.р., р.п. цифры)

Знак для обозначения числа. В математике используют арабские и римские цифры. 

Пример. Сколько разных цифр содержит число 1 020 164? 

прил. цифровой, -ая, -ое, -ые.

(сущ., ср.р., р.п. частного)

1. Результат действия деления, такое число x, что если x = a : b, то bx = a или ax = b. 

2. Выражение a : b или . 

Пример. В записи a : b = c величина c – это частное.

(сущ., ж.р., р.п. части)

1. Доля целого. 

2. Одно из выражений в составе равенства или неравенства. 

Пример. Равенство состоит из двух частей.

прил. частный, -ая, -ое, -ые.

(ср.р., р.п. чётного числа)

Число, которое делится нацело на два. Все чётные числа можно записать как 2n, n ∈ N. 

Пример. Числа 2, 4, 6, 8, … – это чётные числа.

(сущ., м.р., р.п. числителя)

1. Число p, которое стоит над чертой в записи обыкновенной дроби . 

2. Делимое в дроби или дробном выражении. 

Пример. Числитель дроби показывает, сколько частей от единицы мы взяли.

(сущ., ср.р., р.п. числа́, мн. чи́сла)

Понятие, которое служит выражением количества; то, при помощи чего производится счёт предметов и явлений. 

Виды: простое, составное, чётное, нечётное, натуральное, положительное и другие. 

Пример. Приведите пример простого и составного чисел.

прил. числовой, -ая, -ое, -ые.

(ж.р., р.п. числовой оси)

То же, что Координатная ось. 

(ср.р., р.п. числового выражения)

Запись, которая состоит только из чисел, знаков действий и скобок. 

Пример. Найдите значение числового выражения 36 : [15 : (8 – 3) • 4] + 16 : (18 – 5 •2).

(ср.р., р.п. число мнимого числа)

Комплексное число, действительная часть которого равна нулю. 

Пример. Числа 12i, –35i, 6,8i – это число мнимые числа.

(м.р., р.п. члена многочлена)

Одночлен, слагаемое суммы, составляющей многочлен. 

Пример. Многочлен 5x³ – 9x + 2 содержит три члена.

(м.р., р.п. члена пропорции)

Один из элементов пропорции а, b, c, d в пропорции а : b = c : d. Виды: крайний, средний, известный, неизвестный. 

Пример. В пропорции а : b = c : d величины a и d – это крайние члены пропорции, а величины b и c – это средние члены пропорции.

(сущ., м.р., р.п. штриха)

Знак , который помещается справа вверху от буквы или выражения. В дифференциальном исчислении используется для обозначения однократного дифференцирования. С помощью штрихов отличают близкие, но различающиеся объекты, например, вектор до и после преобразования. 

Пример. , .

(сущ., ж.р., р.п. экспоненты)

Показательная функция y = e^x. 

Пример. Постройте график экспоненты.

прил. экспоненциальный, -ая, -ое, -ые.

(сущ., м.р., р.п. экстремума)

Понятие, которое объединяет понятия максимума и минимума. 

Пример. Исследуйте функцию на экстремум.

(сущ., м.р., р.п. элемента)

Объект из совокупности, составляющей рассматриваемое множество. Название множества характеризует основной признак его элементов. 

Пример. Элементами множества натуральных чисел являются натуральные числа.

прил. элементарный, -ая, -ое, -ые.

(ж.р., р.п. элементарной функции)

Функция, полученная из основных элементарных функций (степенной, показательной, логарифмической, тригонометрических и обратных тригонометрических) с помощью четырёх арифметических действий и формирования сложной функции, которые применены конечное число раз. Виды: алгебраическая, трансцендентная. 

Пример. Функция  является элементарной алгебраической на интервале (–1; 1), так как она удовлетворяет уравнению F² + x² = 1.