М
Ма́ксимум ![]()
(сущ., м.р., р.п. максимума)
Значение функции, которое не меньше, чем любое её значение в некоторой окрестности аргумента. ![]()
Пример. В каких точках функция y = sin(x) имеет максимум?
Матема́тика ![]()
(сущ., ж.р., р.п. математики)
Наука о количественных отношениях и пространственных формах действительного мира. ![]()
Пример. Математика – это наука.
прил. математический, -ая, -ое, -ие.
Математи́ческий знак ![]()
(м.р., р.п. математического знака)
1. Символ, который используется в математике и не является цифрой или буквой. ![]()
2. Символ, который обозначает то или иное математическое действие или математическое понятие. ![]()
Пример. Какие математические знаки вы знаете?
Ма́трица ![]()
![]()
(сущ., ж.р., р.п. матрицы)
Прямоугольная таблица, состоящая из элементов, которые расставлены в m строк и n столбцов. Виды: единичная, нулевая, квадратная, прямоугольная и другие. ![]()
Пример. Приведите пример квадратной матрицы третьего порядка.
прил. матричный, -ая, -ое, -ые.
Ме́ньше < ![]()
1. Знак строгого неравенства. ![]()
2. Знак сравнения. ![]()
Пример. 13 < 20.
Ме́ньше и́ли равно́ ≤ ![]()
1. Знак нестрогого неравенства. ![]()
2. Знак сравнения. ![]()
Пример. x ≤ 15.
Ме́тод ![]()
(сущ., м.р., р.п. метода)
Совокупность приёмов или операций для получения искомого результата. ![]()
Пример. Рассмотрим методы решения систем двух линейных уравнений с двумя неизвестными.
Ми́нимум ![]()
(сущ., м.р., р.п. минимума)
Значение функции, которое не больше, чем любое её значение в некоторой окрестности аргумента. ![]()
Пример. В каких точках функция имеет минимум?
Ми́нус – ![]()
1. Знак действия вычитания. ![]()
2. Знак отрицательного числа. ![]()
Пример. Отрицательные числа имеют знак «минус»: –2, –17, –146.
Мни́мая едини́ца ![]()
(ж.р., р.п. мнимой единицы)
Одно из двух чисел, квадрат которых равен числу –1; обозначается буквой i; i2 = –1. ![]()
Пример. i – это мнимая единица.
Мни́мая часть (комплексного числа) ![]()
(ж.р., р.п. мнимой части)
Действительное число b в записи комплексного числа z = a + bi. ![]()
Пример. Мнимая часть комплексного числа обозначается Im z = a.
Многозна́чное число́ ![]()
(ср.р., р.п. многозначного числа)
Число, которое в записи имеет больше одной цифры. ![]()
Пример. 8152, 65, 907 – это многозначные числа.
Многочле́н (полино́м) ![]()
(сущ., м.р., р.п. многочлена)
Сумма произвольного числа одночленов. ![]()
Пример. Приведите пример многочлена третьей степени.
Мно́жество ![]()
(сущ., ср.р., р.п. множества)
Одно из важнейших понятий математики; набор, совокупность, собрание каких-либо объектов (элементов), которые обладают общим для всех характерным свойством. Виды множеств – конечное, бесконечное, пустое, числовое и другие. ![]()
Пример. Пустое множество обозначают знаком ∅.
Мно́жество действи́тельных чи́сел ![]()
![]()
(ср.р., р.п. множества действительных чисел)
Объединение множества рациональных и множества иррациональных чисел. Обозначается буквой R. ![]()
Пример. Множество действительных чисел содержит в себе множества рациональных чисел и множество иррациональных чисел: ![]() .
.
Мно́жество значе́ний фу́нкции ![]()
(ср.р., р.п. множества значений функции)
Множество значений, которое принимает зависимая переменная. ![]()
Пример. Множество значений функции y = x2 – это все неотрицательные числа.
Мно́жество иррациона́льных чи́сел ![]()
(ср.р., р.п. множества иррациональных чисел)
Множество всех бесконечных непериодических дробей. Обозначается буквой J. ![]()
Пример. Множество иррациональных чисел – это подмножество множества действительных чисел: ![]() .
.
Мно́жество натура́льных чи́сел ![]()
![]()
(ср.р., р.п. множества натуральных чисел)
Множество целых положительных чисел. Обозначается буквой N. ![]()
Пример. Множество натуральных чисел – подмножество множества целых чисел:![]() .
.
Мно́жество рациона́льных чи́сел ![]()
![]()
(ср.р., р.п. множества рациональных чисел)
Все бесконечные периодические дроби. Обозначается буквой Q. ![]()
Пример. Множество рациональных чисел – это подмножество множества действительных чисел: ![]() .
.
Мно́жество це́лых чи́сел ![]()
![]()
(ср.р., р.п. множества целых чисел)
Все натуральные числа, им противоположные числа и нуль. Обозначается буквой Z. ![]()
Пример. Множество целых чисел – это подмножество множества рациональных чисел: ![]() .
.
Мно́житель ![]()
![]()
(сущ., м.р., р.п. множителя)
1. Компонента действия умножения. ![]()
2. Число или выражение, на которое в задаче или примере умножается другое число или выражение. ![]()
Пример. В записи a • b = c величина a – это первый множитель, а величина b – это второй множитель.
гл. умножать, умножить
Мо́дуль ![]()
(сущ., м.р., р.п. модуля)
То же, что Абсолютная величина. ![]()
Н
Наибо́льший о́бщий дели́тель чи́сел a и b ![]()
![]()
(м.р., р.п. наибольшего общего делителя чисел a и b)
Наибольшее число, на которое числа a и b делятся нацело. Обозначается НОД(a, b). ![]()
Пример. Наибольший общий делитель чисел 12 и 18 равен числу 6.
Наиме́ньшее о́бщее кра́тное натура́льных чи́сел a и b ![]()
![]()
(м.р., р.п. наименьшего общего кратного натуральных чисел a и b)
Наименьшее число, которое делится нацело и на a, и на b. Обозначается НОК(a, b). ![]()
Пример. Наименьшее общее кратное чисел 12 и 18 равно числу 36.
Направле́ние ![]()
(сущ., ср.р., р.п. направления)
Линия движения чего-нибудь; сторона, в которую развивается действие чего-нибудь или в которой находится что-нибудь. ![]()
Пример. Обозначим на прямой линии направление вправо стрелкой и будем рассматривать это направление как положительное.
гл. направлять, направить.
Натура́льные чи́сла ![]()
![]()
(мн., р.п. натуральных чисел)
Числа, которые используют при счёте предметов. ![]()
Пример. Натуральные числа – это числа 1, 2, 3, 4, … .
Нача́ло коорди́нат ![]()
![]()
![]()
(ср.р., р.п. начала координат)
Точка пересечения осей координат, которая является началом отсчёта. Обозначается буквой О. ![]()
Пример. График функции y = sin x проходит через начало координат.
Не иметь смы́сла ![]()
(гл., несов.) не иметь I (чего?) смысла
Для выражений: не иметь числового значения. ![]()
Пример. Если числовое выражение содержит деление на нуль, то говорят, что числовое выражение не имеет смысла.
Не принадлежи́т ∉ ![]()
Знак непринадлежности элемента множеству. ![]()
Пример. Запись a ∉ Z означает, что a не является элементом множества Z.
Не равно́ ≠ ![]()
Знак неравенства. ![]()
Пример. y ≠ 1.
Неве́рное нера́венство ![]()
(ср.р., р.п. неверного неравенства)
Неравенство, логическое значение которого – ложь. ![]()
Пример. 15 > 11 – это неверное неравенство.
Неве́рное ра́венство ![]()
(ср.р., р.п. неверного равенства)
Равенство, где левая и правая части имеют различные значения. ![]()
Пример. 16 = 23 – это неверное равенство.
Неизве́стная величина́ ![]()
(ж.р., р.п. неизвестной величины)
Величина в уравнении, которая обозначена буквой. Значение неизвестной величины необходимо найти. ![]()
Пример. корень уравнения – это значение неизвестной величины, которое обращает уравнение в верное числовое равенство.
Ненатура́льное число́ ![]()
(ср.р., р.п. ненатурального числа)
Число, которое не является натуральным, которое не принадлежит множеству натуральных чисел. ![]()
Пример. 1. Нуль – это ненатуральное число.
2. Все отрицательные числа – это ненатуральные числа.
Неопределённый интегра́л фу́нкции f (x) ![]()
(м.р., р.п. неопределённого интеграла функции f (x))
Совокупность первообразных функций, имеющих одну и ту же производную; обозначается ![]() .
. ![]()
Пример. Запомните таблицу неопределённых интегралов основных элементарных функций.
Неотрица́тельное число́ ![]()
(ср.р., р.п. неотрицательного числа)
Число, которое больше или равно числу нуль. ![]()
Пример. Все числа из множества ![]() – это неотрицательные числа.
– это неотрицательные числа.
Непаралле́льные прямы́е ![]()
(сущ., м.р., р.п. модуля)
Прямые, которые не являются параллельными. ![]()
Пример. Покажите на чертеже непараллельные прямые.
Неперпендикуля́рные прямы́е ![]()
(сущ., м.р., р.п. модуля)
Прямые, которые не являются перпендикулярными. ![]()
Пример. Покажите на чертеже неперпендикулярные прямые.
Непра́вильная дробь ![]()
(ж.р., р.п. неправильной дроби)
Дробь, у которой числитель больше или равен её знаменателю. ![]()
Пример. 1. Дроби ![]() – это неправильные дроби.
– это неправильные дроби.
2. Неправильную дробь можно записать как смешанную.
Нера́венство ![]()
(сущ., ж.р., р.п. неравенства)
Запись (формула), которая состоит из двух выражений, соединённых знаками >, ≥, <, ≤, ≠. Виды: верное, неверное, двойное, строгое, нестрогое. ![]()
Пример. Запись 2 + 5 < 10 – строгое верное неравенство.
Несократи́мая дробь ![]()
(ж.р., р.п. несократимой дроби)
Дробь, у которой числитель и знаменатель не имеют общих простых делителей. ![]()
Пример. Дроби ![]() – это несократимые дроби.
– это несократимые дроби.
Нечётное число́ ![]()
(ср.р., р.п. нечётного числа)
Число, которое не делится нацело на два. ![]()
Пример. 1. 3 – это нечётное число.
2. Все нечётные числа можно записать как 2n – 1, n ∈ Z.
Но́мер ![]()
(сущ., м.р., р.п. номера)
Натуральное число, которое соответствует данному элементу последовательности. ![]()
Пример. Элемент последовательности xn имеет номер n.
О
О́бласть ![]()
(сущ., ж.р., р.п. области)
Непустое множество точек. ![]()
Пример. 1. Область допустимых значений выражения ![]() – все действительные числа, кроме чисел ±1:
– все действительные числа, кроме чисел ±1: ![]() .
.
2. Область определения функции ![]() – все неотрицательные числа:
– все неотрицательные числа: ![]() .
.
О́бласть допусти́мых значе́ний переме́нной ![]()
(ж.р., р.п. области допустимых значений переменной)
Множество всех допустимых значений переменных выражения. ![]()
Пример. Область допустимых значений выражения ![]() – все действительные числа, кроме чисел ±2:
– все действительные числа, кроме чисел ±2: ![]() .
.
О́бласть определе́ния фу́нкции ![]()
(ж.р., р.п. области определения функции)
Множество всех действительных значений аргумента, при которых функция может иметь действительное значение. ![]()
Пример. Область определения функции ![]() – все положительные числа:
– все положительные числа: ![]() .
.
Обра́тная дробь ![]()
(ж.р., р.п. обратной дроби)
Дробь ![]() – это дробь, обратная для дроби
– это дробь, обратная для дроби ![]() .
. ![]()
Пример. Найдите обратную дробь для дроби ![]() .
.
Обра́тная тригонометри́ческая фу́нкция ![]()
![]()
![]()
![]()
![]()
(ж.р., р.п. обратной тригонометрической функции)
Одна из основных элементарных функций, арксинус y = arcsin x, арккосинус y = arccos x, арктангенс y = arctg x и арккотангенс y = arcctg x. ![]()
Пример. Назовите обратные тригонометрические функции.
Обра́тно пропорциона́льные величи́ны ![]()
(мн., р.п. обратно пропорциональных величин)
Такие величины x и y, что при увеличении величины x в несколько раз величина y уменьшается во столько же раз. ![]()
Пример. Величины x и ![]() – обратно пропорциональные.
– обратно пропорциональные.
Обра́тное число́ ![]()
(ж.р., р.п. обратного числа)
Для числа q ≠ 0 – это число ![]() . Произведение числа q и обратного числа
. Произведение числа q и обратного числа ![]() равно единице.
равно единице. ![]()
Пример. Числа q и ![]() – взаимно обратные числа.
– взаимно обратные числа.
О́бщий мно́житель ![]()
(м.р., р.п. общего множителя)
Множитель (число или выражение), одинаковый в нескольких слагаемых. ![]()
Пример. Вынесите общий множитель за скобки.
Обыкнове́нная дробь ![]()
(ж.р., р.п. обыкновенной дроби)
Число, которое можно записать в виде ![]() («пэ кутых»), где
(«пэ кутых»), где ![]() .
. ![]()
Пример. Числа ![]() – это обыкновенные дроби.
– это обыкновенные дроби.
Однозна́чное число́ ![]()
(ср.р., р.п. однозначного числа)
Число, которое записано с помощью одной цифры. ![]()
Пример. Числа 1, 2, 3,…, 9 – это однозначные числа.
Одночле́н ![]()
(сущ., м.р., р.п. одночлена)
Целое алгебраическое выражение, которое содержит числа, переменные и только действия умножение и возведение в целую неотрицательную степень. ![]()
Пример. Подобные одночлены имеют одинаковую буквенную часть и могут отличатся только коэффициентами.
Окру́жность ![]()
![]()
(сущ., ж.р., р.п. окружности, мн. окружности)
Множество всех точек плоскости, которые находятся на одном и том же положительном расстоянии R от данной точки O этой плоскости. Здесь R – радиус окружности, точка O – центр окружности. ![]()
Пример. Постройте окружность с центром в начале координат и радиусом 5см.
Определённый интегра́л фу́нкции f (x) от a до b ![]()
(м.р., р.п. определённого интеграла функции f (x) от a до b)
Разность F(b) – F(a), где F(x) – любая из первообразных; обозначается ![]() .
. ![]()
Пример. Определённый интеграл используют, чтобы найти площадь криволинейной трапеции.
Определи́тель (квадратной матрицы) ![]()
(сущ., м.р., р.п. определителя)
Сумма всех возможных для данной квадратной матрицы членов определителя, которые взяты со своими знаками. ![]()
Пример. Определитель квадратной матрицы второго порядка вычисляют по формуле ![]()
Ордина́та ![]()
![]()
![]()
(сущ., ж.р., р.п. ординаты)
Вторая по порядку из координат точки на плоскости или в пространстве; обозначается буквой y. ![]()
Пример. 1. Ордината точки A(3; 4) равна числу 4.
2. Ордината точки B(2; 6; 1) равна числу 6.
Основа́ние логари́фма ![]()
(ср.р., р.п. основания логарифма)
Такое положительное число, отличное от единицы, которое при возведении в степень, показатель которой равен логарифму, даёт подлогарифмическое выражение: ![]() .
. ![]()
Пример. В записи x = logab величина a – это основание логарифма.
Основа́ние сте́пени ![]()
(ср.р., р.п. основания степени)
Компонента действия возведения в степень, которую повторяют заданное число раз при умножении: ![]()
![]()
Пример. В записи an = b величина a – это основание степени.
Оста́ток от деле́ния ![]()
(м.р., р.п. остатка от деления)
1. Наименьшее положительное число, которое можно получить из делимого, вычитая из него различные кратные делителя. ![]()
2. Составная часть результата действия деления с остатком. ![]()
Пример. Деление с остатком: 14 : 3 = 4 (остаток 2).
О́стрый у́гол ![]()
![]()
(м.р., р.п. острого угла)
Угол, который больше 0°, но меньше 90°. ![]()
Пример. Угол 45° – это острый угол.
Ось ![]()
![]()
(сущ., ж.р., р.п. оси)
Прямая, на которой задано положительное направление. ![]()
Пример. Начало отсчёта (начальная точка) О делит координатную ось на два луча.
прил. осевой, -ая, -ое, -ые.
Ось абсци́сс ![]()
![]()
(ж.р., р.п. оси абсцисс)
Первая из осей декартовой систем координат на плоскости или в пространстве. ![]()
Пример. Ось абсцисс принято обозначать Ox.
Ось апплика́т ![]()
![]()
(ж.р., р.п. оси аппликат)
Третья из осей декартовой системы координат в пространстве. ![]()
Пример. Ось аппликат принято обозначать Oz.
Ось ордина́т ![]()
![]()
(ж.р., р.п. оси ординат)
Вторая из осей декартовой систем координат на плоскости или в пространстве. ![]()
Пример. Ось ординат принято обозначать Oy.
Отноше́ние величи́н ![]()
(ср.р., р.п. отношения величин)
Выражение a : b, где a и b – некоторые математические величины. ![]()
Пример. Найдите отношение заданных величин.
Отноше́ние чи́сел ![]()
(ср.р., р.п. отношения чисел)
Частное чисел a : b, то есть само выражение a : b и его значение. ![]()
Пример. Отношение чисел a и b равно пяти.
Отре́зок ![]()
(сущ., м.р., р.п. отрезка)
1. Часть прямой, заключённая между двумя её точками и включающая обе точки. Для обозначения отрезка используют прописные буквы латинского алфавита. ![]()
2. Множество действительных чисел x, которые удовлетворяют нестрогому неравенству a ≤ x ≤ b. Для записи отрезков используют квадратные скобки: [a, b]. ![]()
Пример. 1. На прямой найдите отрезок AB.
2. Числовой отрезок – это замкнутый промежуток.
Отрица́тельное направле́ние ![]()
(ср.р., р.п. отрицательного направления)
Направление на числовой оси влево; для декартовой системы координат на оси абсцисс также влево, на оси ординат вниз от начала отсчёта. ![]()
Пример. Покажите отрицательное направление на оси абсцисс.
Отрица́тельное число́ ![]()
(ср.р., р.п. отрицательного числа)
Число со знаком минус; число, меньшее нуля. ![]()
Пример. Отрицательное число меньше нуля.
Отрица́тельный луч ![]()
(м.р., р.п. отрицательного луча)
Координатный луч, который идёт влево (в отрицательном направлении) от точки О (начала отсчёта) на горизонтальной оси и вниз от точки О на вертикальной оси. ![]()
Пример. Какие точки лежат на отрицательном луче?
П
Па́ра ![]()
(сущ., ж.р., р.п. пары)
Два объекта вместе. ![]()
Пример. Назовите пару чисел, которые удовлетворяют заданному условию.
прил. парный, -ая, -ое, -ые.
Пара́бола ![]()
![]()
![]()
(сущ., ж.р., р.п. параболы)
Плоская кривая линия второго порядка, график функции y = ax2 + bx + c. ![]()
Пример. Каноническое уравнение параболы имеет вид: y2 = 2px, где p – параметр.
Паралле́льность ![]()
(сущ., ж.р., р.п. параллельности)
Отсутствие общих точек у двух прямых, лежащих в одной плоскости, или у прямой и плоскости, или у двух плоскостей. ![]()
Пример. Докажите параллельность прямых AB и CD.
сущ. параллель (ж.р.)
прил. параллельный, -ая, -ое, -ые.
Паралле́льные прямы́е ![]()
![]()
(мн., р.п. параллельных прямых)
Прямые, которые лежат в одной плоскости и не имеют общих точек. ![]()
Пример. Запись a || b означает, что a и b – это параллельные прямые.
Переме́нная ![]()
(сущ., м.р., р.п. отрезка)
То же, что Переменная величина. ![]()
Переме́нная величина́ ![]()
(сущ., м.р., р.п. отрезка)
Величина, значение которой в условиях данной задачи может изменяться. ![]()
Пример. Сколько переменных величин содержит выражение 2x2+ 3y2– 2x – 6y?
Пересека́ющиеся прямы́е ![]()
![]()
(мн., р.п. пересекающихся прямых)
Прямые, которые лежат в одной плоскости и имеют одну общую точку. Такую общую точку называют точкой пересечения прямых. ![]()
Пример. Покажите на чертеже пересекающиеся прямые.
Перестано́вка ![]()
(сущ., ж.р., р.п. перестановки)
1. Расположение в определённом порядке элементов конечного множества. ![]()
2. Изменение местоположения объектов. ![]()
Пример. От перестановки слагаемых сумма не изменяется.
гл. переставлять, переставить.
Пери́од ![]()
![]()
(сущ., м.р., р.п. периода)
1. Цифра или группа цифр, которая стоит после запятой и повторяется в записи десятичной периодической дроби бесконечное число раз. ![]()
2. Неравное нулю число, которое при прибавлении к аргументу не изменяет значения функции. ![]()
Пример. 1. Период десятичной дроби 3,(7) – это цифра 7.
2. Период тригонометрической функции y = sin x равен ![]() .
.
прил. периодический, -ая, -ое, -ие.
Периоди́ческая фу́нкция ![]()
![]()
(ж.р., р.п. периодической функции)
Функция, которая имеет отличный от нуля период. ![]()
Пример. Основные тригонометрические функции – это периодические функции.
Перпендикуля́р ![]()
![]()
(сущ., м.р., р.п. перпендикуляра)
Прямая, пересекающая под прямым углом данную прямую. ![]()
Пример. Опустите перпендикуляр из точки А на прямую CD.
прил. перпендикулярный, -ая, -ое, -ые.
Перпендикуля́рность ![]()
(сущ., ж.р., р.п. перпендикулярности)
Взаимное свойство двух прямых, прямой и плоскости или двух плоскостей, которые пересекаются друг с другом и образуют в точке пересечения прямой угол. ![]()
Пример. Докажите перпендикулярность прямых AB и CD.
Перпендикуля́рные прямы́е ![]()
![]()
(мн., р.п. перпендикулярных прямых)
Прямые, которые пересекаются под прямым углом. ![]()
Пример. Запись a ![]() b означает, что a и b – это перпендикулярные прямые.
b означает, что a и b – это перпендикулярные прямые.
Пло́скость ![]()
![]()
(сущ., ж.р., р.п. плоскости)
1. Один из основных объектов геометрии; множество точек, декартовы координаты которых удовлетворяют уравнению ах + by + cz = d, где а, b, с и d – числа, которые одновременно не равны нулю. ![]()
2. Плоская поверхность, такая, что любая прямая, которая соединяет две её точки, целиком принадлежит этой поверхности. ![]()
Пример. Покажите на чертеже параллельные плоскости.
прил. плоский, -ая, -ое, -ие.
плоскостной, -ая, -ое, -ые.
Плюс + ![]()
1. Знак действия сложения. ![]()
2. Знак положительного числа. ![]()
Пример. 1. Какое арифметическое действие имеет знак «плюс»?
2. Положительные числа имеют знак «плюс».
Подкоренно́е выраже́ние ![]()
(ср.р., р.п. подкоренного выражения)
Выражение, которое стоит под знаком корня. ![]()
Пример. В записи ![]() выражение a – это подкоренное выражение.
выражение a – это подкоренное выражение.
Подмно́жество ![]()
(сущ., ср.р., р.п. подмножества)
Множество B, каждый элемент которого принадлежит множеству А. Множество A содержит любое своё подмножество: B ![]() A.
A. ![]()
Пример. Множество всех чётных чисел является подмножеством множества целых чисел.
Подо́бные чле́ны ![]()
(мн., р.п. подобных членов)
Члены многочлена, которые имеют одинаковую буквенную часть (переменные и показатели их степеней) и могут отличаться только коэффициентом. ![]()
Пример. Приведите подобные члены в выражении 5ab + 4ab2 – ab – 12ab2.
Показа́тель ![]()
(сущ., м.р., р.п. показателя)
Аргумент показательной функции – второй из элементов, которые участвуют в действии возведения в степень. ![]()
Пример. Как возвести число в степень с дробным показателем?
Показа́тель ко́рня ![]()
![]()
(м.р., р.п. показателя корня)
В записи ![]() , n – это показатель корня.
, n – это показатель корня. ![]()
Пример. Показатель корня – это натуральное число, большее числа 1.
Показа́тель сте́пени ![]()
![]()
(м.р., р.п. показателя степени)
Компонента действия возведения в степень, которая показывает, сколько раз нужно взять множителем основание степени. ![]()
Пример. В записи an = b число n – это показатель степени.
Показа́тельная фу́нкция ![]()
![]()
![]()
(ж.р., р.п. показательной функции)
Функция, которая задана формулой y = ax, где a > 0, a ≠ 1. ![]()
Пример. Экспонента y = ex – пример показательной функции.
Показа́тельное уравне́ние ![]()
(ср.р., р.п. показательного уравнения)
Уравнение, в котором неизвестное входит в показатель степени. Простейшее показательное уравнение имеет вид ax = b (а > 0, a ≠ 1, b > 0). ![]()
Пример. Какие методы решения показательных уравнений вы знаете?
Полино́м ![]()
(сущ., м.р., р.п. полинома)
То же, что Многочлен. ![]()
Положи́тельная дробь ![]()
(ж.р., р.п. положительной дроби)
Дробное число, которое больше нуля. ![]()
Пример. Положительные дробные числа – это положительные обыкновенные дроби.
Положи́тельное направле́ние ![]()
(ср.р., р.п. положительного направления)
Направление на числовой оси вправо; для декартовой системы координат на оси абсцисс также вправо, на оси ординат вверх от начала отсчёта. ![]()
Пример. Укажите на оси абсцисс положительное направление.
Положи́тельное число́ ![]()
(ср.р., р.п. положительного числа)
Число, которое больше нуля и расположено на числовой оси справа от нуля. ![]()
Пример. 1. Положительное число больше нуля.
2. Положительное число имеет знак плюс.
Положи́тельный луч ![]()
![]()
(м.р., р.п. положительного луча)
Координатный луч, который идёт вправо (в положительном направлении) от точки О (начала отсчёта) на горизонтальной оси и вверх от точки О на вертикальной оси. ![]()
Пример. Если точка находится на положительном луче, то она изображает положительное число.
Полуинтерва́л ![]()
(сущ., м.р., р.п. полуинтервала)
Множество чисел x (точек числовой прямой), которые удовлетворяют неравенствам a ≤ x < b или a < x ≤ b. Неравенство a ≤ x < b соответствует полуинтервалу, открытому справа, и обозначается [a, b). Неравенство a < x ≤ b соответствует полуинтервалу, открытому слева и обозначается (a, b]. ![]()
Пример. Прочитайте полуинтервалы.
Полупряма́я ![]()
(сущ., ж.р., р.п. полупрямой)
То же, что Луч. ![]()
Поря́док де́йствий ![]()
(м.р., р.п. порядка действий)
Последовательность, в которой производятся те или иные действия. ![]()
Пример. Определите порядок выполнения арифметических действий в выражении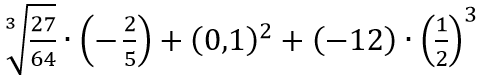 и найдите его значение.
и найдите его значение.
![]()
(сущ., ж.р., р.п. последовательности)
Функция, которая задана на множестве натуральных чисел. Обозначается ![]() .
. ![]()
Пример. Если последовательность задана формулой общего члена, то можно определить значение любого члена последовательности по его номеру.
прил. последовательный, -ая, -ое, -ые.
Постоя́нная величина́ ![]()
(ж.р., р.п. постоянной величины)
Величина, значение которой в условиях данной задачи не может изменяться. ![]()
Пример. Какие постоянные величины используют в математике?
Пра́вая часть ![]()
(ж.р., р.п. правой части)
Выражение, которое стоит справа от знака сравнения (=, ≠, >, <, ≥, ≤). ![]()
Пример. Правая часть равенства стоит справа от знака равно.
Пра́вильная дробь ![]()
(ж.р., р.п. правильной дроби)
Дробь, у которой числитель меньше, чем её знаменатель. ![]()
Пример. Числа ![]() – это правильные дроби.
– это правильные дроби.
Преде́л после́довательности ![]()
![]()
(м.р., р.п. предела последовательности)
Постоянное число a, для которого верно утверждение: для любого сколь угодно малого положительного числа ε, существует такой номер n0, что для любого номера n ≥ n0 выполняется неравенство |xn – a| < ε. ![]()
Пример. Предложение «Предел последовательности xn при n, которое стремится к бесконечности, равен а» записывают так: ![]() .
.
Преде́л фу́нкции y = f(x) в точке a ![]()
(м.р., р.п. предела функции)
Постоянное число b, для которого верно утверждение: для каждого малого положительного числа ε > 0 существует такое малое положительное число δ > 0, что для всех x, которые удовлетворяют неравенству |x – a| < δ, где x ≠ a, выполняется неравенство |f(x) – b| < ε. ![]()
Пример. Предложения «предел функции f (x) при x, который стремится к a, равен b» и «предел функции f (x) в точке x = a равен b» записывают так: ![]() .
.
Преде́льное значе́ние ![]()
(ср.р., р.п. предельного значения)
Значение, к которому стремится величина. ![]()
Пример. В записи ![]() предельное значение величины n – это бесконечность.
предельное значение величины n – это бесконечность.
Приближённо равно́ ![]()
![]()
Знак приближённого равенства. ![]()
Пример. ![]() ,
, ![]() .
.
При́знак ![]()
(сущ., м.р., р.п. отрезка)
Правило или условие для проверки выполнения или невыполнения данного утверждения. ![]()
Пример. Признак делимости чисел на 5.
При́знак дели́мости ![]()
(м.р., р.п. признака делимости)
Правило, которое позволяет судить о делимости без остатка одних натуральных чисел на другие. ![]()
Пример. Назовите признаки делимости чисел на 3 и на 9.
Принадлежи́т ![]()
![]()
Знак принадлежности элемента множеству. ![]()
Пример. Запись a ∈ Z означает, что a является элементом множества Z.
Прираще́ние ![]()
(сущ., ср.р., р.п. приращения)
Разность двух значений переменной величины. ![]()
Пример. При изучении производной рассматривают приращение аргумента и соответствующее ему приращение функции.
Прираще́ние аргуме́нта ![]()
(ср.р., р.п. приращения аргумента)
Разность двух значений аргумента x1 и x2, которые лежат в области определения функции: Δx = x2 – x1. ![]()
Пример. Найдите приращение аргумента.
Прираще́ние фу́нкции ![]()
(ср.р., р.п. приращения функции)
Разность двух значений функции, которые соответствуют значениям аргумента x1 и x2:
Δy = Δf(x) = f(x2) – f(x1). ![]()
Пример. Приращение функции можно записать как Δy = f(x + Δx) – f(x).
Прогре́ссия ![]()
(сущ., ж.р., р.п. прогрессии)
Название некоторых видов числовых последовательностей. Виды: арифметическая, геометрическая. ![]()
Пример. Запишите формулу суммы всех членов геометрической прогрессии.
Произведе́ние ![]()
![]()
(сущ., ср.р., р.п. произведения)
1. Результат действия умножения. ![]()
2. Выражение a • b (или a × b). ![]()
Пример. Найдите произведение всех однозначных натуральных чисел.
Произво́дная фу́нкции y = f(x) в точке x ![]()
(ж.р., р.п. производной функции y = f(x) в точке x)
Предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю (если этот предел существует): ![]() .
. ![]()
Пример. Если производная существует для каждого значения x в области определения функции, то она представляет собой новую функцию от аргумента x.
Промежу́ток ![]()
(сущ., м.р., р.п. промежутка)
Общее название для множества чисел, которые лежат между числами a и b, с включением или без включения одного или обоих чисел aи b. Виды числовых промежутков: конечный бесконечный, замкнутый, открытый, открытый справа, открытый слева. ![]()
Пример. Открытый числовой промежуток – это интервал.
Пропо́рция ![]()
(сущ., ж.р., р.п. пропорции)
Равенство двух отношений a : b = c : d, где ни одно из чисел не равно нулю. ![]()
Пример. Решите пропорцию ![]() .
.
прил. пропорциональный, -ая, -ое, -ые.
Просто́е число́ ![]()
(ср.р., р.п. простого числа)
Натуральное число, которое больше единицы и делится только на 1 и на себя. ![]()
Пример. Простое число имеет ровно два делителя.
Просто́й дели́тель ![]()
(м.р., р.п. простого делителя)
Делитель, равный простому числу. ![]()
Пример. Число 24 имеет только два простых делителя – числа 2 и 3.
Просты́е мно́жители ![]()
(мн., р.п. простых множителей)
Множители, которые являются простыми числами. ![]()
Пример. Разложите число 1065 на простые множители.
Противополо́жные чи́сла ![]()
(мн., р.п. противоположных чисел)
Два числа, которые отличаются только знаком. ![]()
Пример. 1. Противоположные числа имеют одинаковый модуль.
2. 6 и –6 – это противоположные числа.
Проце́нт ![]()
(сущ., м.р., р.п. процента)
Сотая часть от числа; обозначается %. ![]()
Пример. Рассматривают три основных типа задач на проценты.
прил. процентный, -ая, -ое, -ые.
Проце́нтное отноше́ние чи́сел ![]()
(ср.р., р.п. процентного отношения чисел)
Отношение данных чисел, которое умножили на 100%. ![]()
Пример. Найдите процентное отношение чисел a и b.
Пряма́я ![]()
(сущ., ж.р., р.п. прямой)
То же, что Прямая линия. ![]()
Пряма́я ли́ния ![]()
![]()
(ж.р., р.п. прямой линии)
1. Одно из основных понятий геометрии, принятое за аксиому: «через любые две точки проходит прямая и притом только одна». ![]()
2. Множество точек в евклидовой плоскости, прямоугольные декартовы координаты которых удовлетворяют уравнению ax + by + c = 0, где a и b вместе не равны нулю. ![]()
3. Пересечение двух различных плоскостей в евклидовом трёхмерном пространстве. ![]()
Пример. График функции y = kx + b – это прямая линия.
Пря́мо пропорциона́льные величи́ны ![]()
(мн. р.п. прямо пропорциональных величин)
Такие величины x и y, что при увеличении величины x в несколько раз величина y увеличивается во столько же раз. ![]()
Пример. Величины x и y = 5x – это прямо пропорциональные величины.
Прямо́й у́гол ![]()
![]()
(м.р., р.п. прямого угла)
Угол, равный 90o. ![]()
Пример. Координатные оси пересекаются под прямым углом