А
Абсолю́тная величина́ (мо́дуль) ве́ктора ![]()
![]()
(ж.р., р.п. абсолютной величины вектора)
Длина отрезка, изображающего вектор.Пример. Если известны координаты вектора, то его абсолютную величину можно найти по формуле: ![]() .
.
Абсолю́тная величина́ (мо́дуль) действи́тельного числа́ ![]()
(ж.р., р.п. абсолютной величины действительного числа)
Само число, если оно больше нуля, или равно нулю, и число, взятое с противоположным знаком, если оно меньше нуля. ![]()
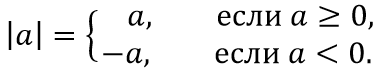
Абсолю́тная величина́ (мо́дуль) компле́ксного числа́ ![]()
![]()
(ж.р., р.п. абсолютной величины комплексного числа)
Расстояние от начала координат комплексной плоскости до точки, изображающей данное комплексное число. ![]()
Абсци́сса ![]()
![]()
![]()
(сущ., ж.р., р.п. абсциссы)
Первая декартова координата точки в системе координат. ![]()
2. Абсцисса точки B(2; 6; 1) равна числу 2.
Аксио́ма ![]()
(сущ., ж.р., р.п. аксиомы)
Исходное предложение, которое принимается без доказательства. ![]()
А́лгебра ![]()
(сущ., ж.р., р.п. алгебры)
Раздел математики, который изучает алгебраические операции над объектами. ![]()
Пример. Элементарная алгебра изучает операции с вещественными числами, содержит преобразования математических выражений и уравнений.
прил. алгебраический, -ая, -ое, -ие
Алгебраи́ческое де́йствие ![]()
(ср.р., р.п. алгебраического действия)
Одна из семи операций над числами: сложение, вычитание, умножение, деление, возведение в степень, извлечение корня, логарифмирование. ![]()
Пример. Логарифмирование – это алгебраическое действие.
Апплика́та ![]()
![]()
(сущ., ж.р., р.п. аппликаты)
Третья декартова координата точки в трёхмерном пространстве. ![]()
Пример. Аппликата точки B(2; 6; 1) равна числу 1.
Арифме́тика ![]()
(сущ., ж.р., р.п. арифметики)
Наука о числах и операциях над ними. ![]()
Пример. Арифметика – это раздел математики, который изучает числа и действия с ними.
прил. арифметический, -ая, -ое, -ие.
Арифмети́ческий ко́рень ![]()
(м.р., р.п. арифметического корня)
Арифметический корень n-ой степени (n ∈ N, n ≠ 1) из неотрицательного числа a (a ≥ 0) – это неотрицательное число b (b ≥ 0), n-ая степень которого равна a, то есть bn = a. ![]()
Пример. Арифметический корень четвёртой степени из числа 16 равен числу 2:![]() .
.
Арифмети́ческое де́йствие ![]()
(ср.р., р.п. арифметического действия)
Одна из четырёх простейших операций над числами: сложение, вычитание, умножение, деление. ![]()
Пример. Сложение – это арифметическое действие: 5 + 14 = 19.
Аркко́синус ![]()
![]()
(сущ., м.р., р.п. арккосинуса)
Обратная тригонометрическая функция y = arccos x, обратная для функции y = cos x на отрезке ![]() .
. ![]()
Пример. Изучите свойства функции арккосинус.
Арккота́нгенс ![]()
![]()
(сущ., м.р., р.п. арккотангенса)
Обратная тригонометрическая функция y = arcctg x, обратная для функции y = ctg x на интервале ![]() .
. ![]()
Пример. Изучите свойства функции арккотангенс.
Аркси́нус ![]()
![]()
(сущ., м.р., р.п. арксинуса)
Обратная тригонометрическая функция y = arcsin x, обратная для функции y = sin x на отрезке ![]() .
. ![]()
Пример. Изучите свойства функции арксинус.
Аркта́нгенс ![]()
![]()
(сущ., м.р., р.п. арктангенса)
Обратная тригонометрическая функция y = arctg x, обратная для функции y = tg x на интервале ![]() .
. ![]()
Пример. Изучите свойства функции арктангенс.
Асимпто́та криво́й ![]()
![]()
![]()
![]()
(ж.р., р.п. асимптоты кривой)
Прямая, к которой приближается как угодно близко точка кривой при удалении в бесконечность. ![]()
Пример. 1. Гипербола ![]() имеет две асимптоты – прямые y = 0 и x = 0.
имеет две асимптоты – прямые y = 0 и x = 0.
2. Парабола y = x2 не имеет асимптот.
Ассоциати́вный зако́н сложе́ния ![]()
(м.р., р.п. ассоциативного закона сложения)
Чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего чисел. То есть для любых трёх чисел a, b и с верно равенство: (a + b) + c = a + (b + c). ![]()
Пример. Ассоциативный закон сложения используют, чтобы упростить вычисления.
Ассоциати́вный зако́н умноже́ния ![]()
(м.р., р.п. ассоциативного закона умножения)
Чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего чисел. То есть для любых чисел a, b и с верно равенство: (ab)c = a(bc). ![]()
Пример. Ассоциативный закон умножения используют, чтобы упростить вычисления.
Б
Бесконе́чная десяти́чная дробь ![]()
(ж.р., р.п. бесконечной десятичной дроби)
Десятичная дробь, у которой после запятой стоит бесконечно много цифр. ![]()
Пример. Числа 0,171717…, 0,10110111011110… – это бесконечные десятичные дроби.
Бесконе́чная непериоди́ческая дробь ![]()
(ж.р., р.п. бесконечной непериодической дроби)
Бесконечная десятичная дробь, у которой никакая группа цифр не является периодом. ![]()
Пример. Числа 0,01001000100001…, 17,12345678910111213…, π = 3,14159265358979323846264…, e = 2,71828182845904523536… – это бесконечные непериодические дроби.
Бесконе́чная периоди́ческая дробь ![]()
(ж.р., р.п. бесконечной периодической дроби)
Десятичная дробь, у которой после запятой стоит бесконечно много раз повторяющаяся цифра (группа цифр). ![]()
Пример. Числа 0,171717… = 0,(17), 3,17777… = 3,1(7) – это бесконечные периодические дроби.
Бесконе́чно больша́я величина́ ![]()
(ж.р., р.п. бесконечно большой величиной)
Переменная величина, которая в процессе своего изменения становится и при дальнейшем изменении остаётся по абсолютной величине больше любого заранее заданного числа A > 0. ![]()
Пример. Величина x = n2 при n → ∞ является бесконечно большой величиной.
Бесконе́чно ма́лая величина́ ![]()
(ж.р., р.п. бесконечно малой величиной)
Переменная величина, которая в процессе своего изменения становится и при дальнейшем изменении остаётся по абсолютной величине меньше любого заранее заданного числа ε > 0. ![]()
Пример. Величина ![]() при n → ∞ является бесконечно малой величиной.
при n → ∞ является бесконечно малой величиной.
Бесконе́чность ![]()
(сущ., ж.р., р.п. бесконечности)
Понятие, которое возникает в различных разделах математики как противопоставление понятию конечного. ![]()
Пример. Бесконечность обозначают знаком ∞.
прил. бесконечный, -ая, -ое, -ые.
нареч. бесконечно.
Бино́м ![]()
(сущ., м.р., р.п. бинома)
То же, что Двучлен. ![]()
Бо́льше > ![]()
1. Знак строгого неравенства. ![]()
2. Знак сравнения. ![]()
Пример. 5 > 8.
Бо́льше и́ли равно́ ≥ ![]()
1. Знак нестрогого неравенства. ![]()
2. Знак сравнения. ![]()
Пример. a ≥ 7.
В
Ве́ктор ![]()
![]()
(сущ., м.р., р.п. ве́ктора, мн. ве́кторы)
Направленный отрезок прямой в евклидовом пространстве. ![]()
Пример. ![]() – вектор с началом в точке A и концом в точке B.
– вектор с началом в точке A и концом в точке B.
прил. векторный, –ая, -ое, -ые.
Величина́ ![]()
(сущ., ж.р., р.п. величины́, мн. величи́ны)
Одно из основных понятий математики; результат измерения. Виды величин – постоянная, переменная, известная, неизвестная, независимая, зависимая, абсолютная и другие. ![]()
Пример. Найдите значение неизвестной величины x из уравнения
3log5 2 + 2 – x = log5 (3x – 52–x).
Ве́рное ра́венство ![]()
(ср.р., р.п. верного равенства)
Равенство, в котором левая и правая части имеют одинаковое значение. ![]()
Взаи́мно обра́тные чи́сла ![]()
(мн., р.п. взаимно обратных чисел)
Два числа a ≠ 0 и ![]() . Произведение взаимно обратных чисел равно числу один (единице).
. Произведение взаимно обратных чисел равно числу один (единице). ![]()
Пример. 2 и ![]() – это взаимно обратные числа,
– это взаимно обратные числа, ![]() .
.
Взаи́мно просты́е чи́сла ![]()
(мн., р.п. взаимно простых чисел)
Два числа, которые не имеют общих простых делителей. ![]()
Пример. 14 и 17 – это взаимно простые числа, НОД(14, 17) = 1.
Возведе́ние в сте́пень ![]()
(ср.р., р.п. возведения в степень)
Возведение в степень числа a с натуральным показателем n (n > 1) – это нахождение произведения n множителей, каждый из которых равен a. ![]()
Пример. Возвести число в натуральную степень можно по формуле ![]()
гл. возводить, возвести.
Возраста́ние фу́нкции ![]()
![]()
(ср.р., р.п. возрастания функции)
Свойство функции, при котором большему значению аргумента соответствует большее значение функции. ![]()
Пример. Определите промежутки возрастания функции y = sin x.
гл. возрастать.
Возраста́ющая фу́нкция ![]()
![]()
![]()
(ж.р., р.п. возрастающей функции)
Такая функция y = f (x), у которой для любых x1, x2 ∈ (a, b) при x1 < x2 верно неравенство f (x1) < f (x2). ![]()
Пример. Функция y = x2 при x > 0 возрастает.
Вынесе́ние о́бщего мно́жителя за ско́бки ![]()
![]()
(ср.р., р.п. вынесения общего множителя за скобки)
Переход от записи вида ab + ac к записи вида a(b + c). ![]()
Пример. Чтобы выполнить вынесение общего множителя за скобки, используют дистрибутивный закон умножения.
гл. выносить, вынести.
Выраже́ние ![]()
(сущ., ср.р., р.п. выражения)
Формула или её часть. Виды выражений – числовое выражение, выражение с переменной. ![]()
Пример. 5 • 10 + 7 – это числовое выражение.
гл. выражать, выразить.
Выраже́ние с переме́нной ![]()
(ср.р., р.п. выражения с переменной)
Выражение, которое состоит из чисел, знаков действий, скобок, постоянных или переменных величин. ![]()
Пример. 2x + 7 – это выражение с переменной.
Вычита́емое ![]()
![]()
(сущ., ср.р., р.п. вычитаемого)
Число, которое вычитается из другого числа; вторая компонента действия вычитания. ![]()
Пример. В записи a + b = c величина b – это вычитаемое.
Вычита́ние ![]()
![]()
(сущ., ср.р., р.п. вычитания)
Операция, обратная сложению. Вычитание позволяет по сумме и одному из слагаемых находить другое слагаемое. Если a + b = c, то a = c – b и b = c – a. ![]()
Пример. Вычитание – это арифметическое действие, обратное сложению.
Г
Геоме́трия ![]()
(сущ., ж.р., р.п. геометрии)
Раздел математики, который изучает пространственные отношения и формы тел и их обобщения. ![]()
Пример. 1. Геометрия – раздел математики.
2. Примеры геометрий – геометрия Евклида, геометрия Лобачевского.
прил. геометрический, -ая, -ое, -ие.
Гипе́рбола ![]()
![]()
![]()
(сущ., ж.р., р.п. гиперболы)
Кривая линия второго порядка, график функции ![]() .
. ![]()
Пример. Каноническое уравнение гиперболы имеет вид: ![]() , где a – действительная полуось, b – мнимая полуось гиперболы.
, где a – действительная полуось, b – мнимая полуось гиперболы.
Гипотену́за ![]()
![]()
(сущ., м.р., р.п. гипотенузы)
Сторона прямоугольного треугольника, которая лежит против прямого угла. ![]()
Пример. Найдите гипотенузу прямоугольного треугольника, если известны его катеты.
Гра́дус ![]()
(сущ., м.р., р.п. градуса)
Единица измерения плоских углов, равная ![]() части прямого угла. Полная окружность содержит 360°.
части прямого угла. Полная окружность содержит 360°. ![]()
Пример. Величина прямого угла 90°.
Гра́фик фу́нкции ![]()
![]()
(м.р., р.п. графика функции)
Множество всех точек плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции. ![]()
Пример. Графиком функции y = x2 является парабола.
Д
Двучле́н (бино́м) ![]()
(сущ., м.р., р.п. двучлена)
Многочлен, у которого только два члена. ![]()
Пример. a + b – это двучлен.
Действи́тельная часть (комплексного числа) ![]()
(ж.р., р.п. действительной части)
Действительное число a в записи комплексного числа z = a + bi. ![]()
Пример. Действительная часть комплексного числа обозначается Re z = a.
Действи́тельные чи́сла ![]()
![]()
(мн., р.п. действительных чисел)
1. Все рациональные и иррациональные числа. ![]()
2. Бесконечные десятичные периодические и непериодические дроби. ![]()
Пример. Действительные числа также называются вещественными числами.
Деле́ние ![]()
![]()
(сущ., ср.р., р.п. деления)
Арифметическое действие, обратное действию умножение. Деление позволяет по данному произведению и одному из множителей найти другой множитель. Если a • b = c и b ≠ 0, то a = c : b. Знаки действия деления – разделить «:», косая черта «/», обелюс «÷». Компоненты – делимое и делитель, результат – частное или неполное частное и остаток. Виды деления – деление нацело и деление с остатком. ![]()
Пример. Выполните деление заданных чисел на 2.
гл. делить, разделить.
Деле́ние на́цело ![]()
(ср.р., р.п. деления нацело)
Нахождение по двум заданным целым числам a и b (b ≠ 0) частного x так, чтобы выполнялось равенство a = bx, где x – целое число. ![]()
Пример. Выполните деление нацело числа 154 на число 3.
Деле́ние с оста́тком ![]()
(ср.р., р.п. деления с остатком)
Нахождение по двум заданным целым числам a и b (b ≠ 0) неполного частного x и остатка y так, чтобы выполнялось равенство a = bx + y, 0 ≤ y < b, где x, y – целые числа. ![]()
Пример. Выполните деление с остатком числа 271 на число 5.
Дели́мое ![]()
![]()
(сущ., ср.р., р.п. делимого)
Число, которое делят на другое число; первая компонента действия деления. ![]()
Пример. В записи a : b = cвеличина a – это делимое.
Дели́мость ![]()
(сущ., ж.р., р.п. делимости)
Свойство целого числа делиться без остатка (нацело) на заданное число. ![]()
Пример. Признак делимости чисел на 10: если последняя цифра числа – нуль, то число делится нацело на 10.
Дели́тель ![]()
![]()
(сущ., м.р., р.п. делителя)
1. Число, на которое делят другое число; вторая компонента действия деления. ![]()
2. Делитель целого числа a – целое число b, на которое число a делится нацело (без остатка). ![]()
Пример. 1. В записи a : b = cвеличина b – это делитель. 2. Запишите все делители числа 100.
Десяти́чная дробь ![]()
(ж.р., р.п. десятичной дроби)
Дробь, у которой знаменатель является степенью числа 10. Такую дробь записывают в более простой форме, без знаменателя. В десятичной дроби целую и дробную части друг от друга отделяют знаком «,». ![]()
Пример. Числа 1,2; 0,05; 703,0302 – это десятичные дроби.
Десяти́чная запя́тая ![]()
(ж.р., р.п. десятичной запятой)
Знак, который используют для того, чтобы отделить целую часть от дробной части при записи действительного числа в виде десятичной дроби. ![]()
Пример. Дробная часть десятичной дроби стоит после десятичной запятой.
Дискрими́нант трёхчле́на ax2 + bx + c (a ≠ 0) ![]()
(м.р., р.п. дискриминанта трёхчлена)
Число D (Δ) = b2 – 4ac. ![]()
Пример. Значение дискриминанта определяет количество корней квадратного трёхчлена.
Дистрибути́вный зако́н умноже́ния ![]()
(м.р., р.п. дистрибутивного закона умножения)
Чтобы число умножить на сумму двух чисел, можно это число умножить на каждое слагаемое и полученные произведения сложить. То есть для любых натуральных чисел a, b и с верно равенство: a(b + c) = ab + ac. ![]()
Пример. Дистрибутивный закон умножения используют, чтобы раскрыть скобки и вынести общий множитель за скобки.
Дифференциа́л ![]()
(сущ., м.р., р.п. дифференциала)
Главная линейная часть приращения функции y = f '(x). Обозначается dy = f '(x)dx. ![]()
Пример. Найдите дифференциал заданной функции.
прил. дифференциальный, -ая, -ое, -ые
гл. дифференцировать, продифференцировать
Дифференци́рование ![]()
(сущ., ср.р., р.п. дифференцирования)
Вычисление дифференциалов или производных функций. ![]()
Пример. Выполните дифференцирование.
Длина́ отре́зка ![]()
![]()
(ж.р., р.п. длины отрезка)
Расстояние между концами отрезка. ![]()
Пример. Найдите длину отрезка AB.
Доказа́тельство ![]()
(сущ., ср.р., р.п. доказательства)
Способ обоснования истинности суждения. Виды: от противного, по индукции. ![]()
Пример. Приведите доказательство теоремы Пифагора.
гл. доказывать, доказать.
Допусти́мое значе́ние переме́нной ![]()
(ср.р., р.п. допустимого значения переменной)
Числовое значение переменной выражения, при котором выражение имеет смысл (имеет числовое значение). ![]()
Пример. Найдите все допустимые значения переменных выражения  .
.
Дро́бная часть ![]()
(ж.р., р.п. дробной части)
1. Правильная дробь в составе смешанной дроби. ![]()
2. Число, образованное цифрами, которые стоят после запятой в записи десятичной дроби. ![]()
Пример. Дробная часть числа ![]() – это число
– это число ![]() .
.
Дро́бное число́ ![]()
(ср.р., р.п. дробного числа)
Число, которое записано в виде обыкновенной или десятичной дроби. ![]()
Пример. Числа 1,6 и ![]() – это дробные числа.
– это дробные числа.
Дро́бно-рациона́льное выраже́ние ![]()
(ср.р., р.п. дробно-рационального выражения)
Дробь, у которой числитель и знаменатель – это многочлены с рациональными (целыми) коэффициентами. ![]()
Пример. Дробь ![]() – это дробно-рациональное выражение.
– это дробно-рациональное выражение.
Дробь ![]()
(сущ., ж.р., р.п. дро́би, мн. дро́би)
Число, состоящее из одной или нескольких равных частей единицы. Виды дробей – обыкновенная, правильная, неправильная, смешанная, десятичная и другие. ![]()
Пример. Приведите примеры смешанных дробей.
прил. дробный, -ая, -ое, -ые.
гл. дробить, раздробить.
Е
Едини́ца ![]()
(сущ., ж.р., р.п. единицы)
Наименьшее натуральное число или один. ![]()
Пример. Правильная обыкновенная дробь меньше единицы, а неправильная обыкновенная дробь больше единицы.
прил. единичный, -ая, -ое, -ые.
Едини́ца длины́ ![]()
![]()
(ж.р., р.п. единицы длины)
1. Мера длины, метр. ![]()
2. Отрезок ОЕ на числовой оси, длина которого равна единице. ![]()
Пример. Прямая, на которой выбраны начало отсчёта, положительное направление и единица длины, называется координатной осью.
Едини́ца измере́ния ![]()
(ж.р., р.п. единицы измерения)
Конкретная величина, определённая и принятая по соглашению, с которой сравниваются другие величины того же вида, чтобы выразить их значение относительно данной величины. ![]()
Пример. Назовите единицу измерения длины.
Едини́чная окру́жность ![]()
![]()
(ж.р., р.п. единичной окружности)
Окружность с центром в начале координат и радиусом 1. ![]()
Пример. Единичная окружность используется при определении тригонометрических функций действительного аргумента.
Едини́чный отре́зок ![]()
![]()
(м.р., р.п. единичного отрезка)
Отрезок, отложенный на координатной оси вправо от начала отсчёта и принятый за единицу длины. ![]()
Пример. Отложите на координатных осях равные единичные отрезки.
З
Зави́симость ![]()
(сущ., ж.р., р.п. зависимости)
Наличие определённой связи между различными величинами. ![]()
Пример. Зависимость значения функции от значения аргумента, прямо пропорциональная зависимость, обратно пропорциональная зависимость.
прил. зависимый, -ая, -ое, -ые
гл. зависеть
Зада́ча ![]()
(сущ., ж.р., р.п. задачи)
Требование определить математический объект, который удовлетворяет заданным условиям. ![]()
Пример. Решите задачу нахождения корней квадратного уравнения.
Зако́н ![]()
(сущ., м.р., р.п. закона)
1. Математическая формула (или правило), которую можно доказать или доказывать не надо. ![]()
2. Аксиомы и теоремы теорий, предметом рассмотрения которых являются объекты, которые задаются и объясняются этими теориями. ![]()
Пример. Назовите законы сложения.
прил. законный, -ая, -ое, -ые.
Заме́на переме́нных ![]()
(ж.р., р.п. замены переменных)
Переход от одной системы переменных к другой при решении различных математических задач. ![]()
Пример. Выполните замену переменной при решении иррационального уравнения.
гл. заменять, заменить.
Запята́я ![]()
(сущ., ж.р., р.п. запятой)
Знак, который используют в математике для отделения друг от друга выражений, чисел или их частей. ![]()
Пример. В десятичной дроби целую и дробную части друг от друга отделяют запятой.
Знак ![]()
(сущ., м.р., р.п. знака)
То же, что Математический знак. ![]()
Знамена́тель (обыкновенной дроби) ![]()
(сущ., м.р., р.п. знаменателя)
1. Натуральное число, которое стоит под чертой в записи обыкновенной дроби. ![]()
2. Делитель в дроби или дробном выражении. ![]()
Пример. Знаменатель дроби показывает, на сколько частей мы разделили число один (единицу).
Значе́ние ![]()
(сущ., ср.р., р.п. значения)
Элемент области значений или области определения функции. ![]()
Пример. Для заданного значения аргумента найдите соответствующее значение функции.
гл. значить
Значе́ние аргуме́нта ![]()
![]()
(ср.р., р.п. значения аргумента)
Число, элемент области определения функции, которое принимает данный аргумент. ![]()
Пример. При каких значениях аргумента функция y = x3 принимает положительные значения?
Значе́ние выраже́ния ![]()
(ср.р., р.п. значения выражения)
Числовой результат выражения. ![]()
Пример. Найдите значение числового выражения 36 : [15 : (8 – 3) • 4] + 16 : (18 – 5 •2).
Значе́ние переме́нной ![]()
(ср.р., р.п. значения переменной)
Число, элемент множества значений переменной, которому равна данная переменная. ![]()
Пример. При каких значениях переменных выражение  имеет смысл?
имеет смысл?
Значе́ние фу́нкции ![]()
(ср.р., р.п. значения функции)
Число, элемент множества значений функции, которое принимает данная функция. ![]()
Пример. Найдите значение функции для заданного значения аргумента.
И
Изве́стная величи́на ![]()
(ж.р., р.п. известной величины)
Величина, которая известна, то есть дана в условии задачи. ![]()
Пример. Назовите известные величины данной задачи.
Извлече́ние ко́рня ![]()
![]()
(ср.р., р.п. извлечения корня)
Алгебраическое действие, обратное действию возведения в степень, когда по данной степени и показателю степени надо найти основание степени. Действие извлечения корня обозначают знаком радикала ![]() .
. ![]()
Пример. Возведение в степень и извлечение корня – это обратные действия.
гл. извлекать, извлечь
Извле́чь ко́рень ![]()
(гл., сов.) извлечь I (что?) корень, несов. извлекать I (что?)
Извлечь корень степени n из числа a – это значит найти такое число x, которое при возведении в степень n даёт число a. ![]()
Пример. Что значит извлечь корень степени n из числа a?
Измере́ние ![]()
(сущ., ср.р., р.п. измерение)
Нахождение значения величины опытным путем с помощью специальных технических средств. ![]()
Пример. Для чего используют измерение?
гл. измерять, измерить
Иметь смысл ![]()
(гл., несов.) иметь I (что?) смысл
Иметь числовое значение (для выражений). ![]()
Пример. При каких значениях переменных выражение с переменными имеет смысл?
Интегра́л ![]()
(сущ., м.р., р.п. интеграла)
Важнейшее понятие математического анализа, которое объединяет два понятия – неопределённый интеграл и определённый интеграл. ![]()
Пример. Интеграл обозначают символом ![]() .
.
прил. интегральный, -ая, -ое, -ые.
гл. интегрировать, проинтегрировать
Интегри́рование ![]()
(сущ., ср.р., р.п. интегрирования)
Нахождение неопределённого или определённого интеграла. ![]()
Пример. Назовите методы интегрирования.
Интерва́л ![]()
(сущ., м.р., р.п. интервала)
Множество действительных чисел x, которые удовлетворяют строгому двойному неравенству a < x < b, где a, b – действительные числа, концы интервала. ![]()
Пример. 1. Интервал обозначается (a; b) или ]a; b[.
2. Интервал – это числовой промежуток.
3. Промежуток (a; +∞) – это бесконечный интервал.
прил. интервальный, -ая, -ое, -ые.
Иррациона́льное выраже́ние ![]()
(ср.р., р.п. иррационального выражения)
Выражение, содержащее переменную под знаком корня (радикала). ![]()
Пример. Найдите область допустимых значений переменных иррационального выражения ![]() .
.
Иррациона́льное нера́венство ![]()
(ср.р., р.п. иррационального неравенства)
Неравенство, которое содержит переменную под знаком радикала. ![]()
Пример. Решите иррациональное неравенство ![]() .
.
Иррациона́льное уравне́ние ![]()
(ср.р., р.п. иррационального уравнения)
Уравнение, которое содержит неизвестное под знаком радикала. ![]()
Пример. Решите иррациональное уравнение ![]() .
.
Иррациона́льное число́ ![]()
(ср.р., р.п. иррационального числа)
Число, которое записано в виде бесконечной непериодической десятичной дроби. ![]()
Пример. Все иррациональные числа образуют множество иррациональных чисел J.
Иррациона́льность ![]()
(сущ., ж.р., р.п. иррациональности)
1. Наличие в алгебраическом выражении радикала с натуральным показателем. ![]()
2. Иррациональное выражение или число. ![]()
Пример. Освободите от иррациональности знаменатель дроби  .
.
прил. иррациональный, -ая, -ое, -ые.
К
Ка́тет ![]()
![]()
(сущ., м.р., р.п. катета)
Сторона прямоугольного треугольника, которая прилегает к прямому углу. ![]()
Пример. Найдите катет прямоугольного треугольника, если известны его гипотенуза и второй катет.
Квадра́тная ма́трица ![]()
(ж.р., р.п. квадратной матрицы)
Матрица, которая имеет одинаковое число строк и столбцов. ![]()
Пример. Квадратная матрица третьего порядка имеет вид  .
.
Квадра́тное нера́венство ![]()
(ср.р., р.п. квадратного уравнения)
Неравенство вида ax2 + bx + с R 0 (a ≠ 0), где R ![]() {>, ≥, <, ≤}.
{>, ≥, <, ≤}. ![]()
Пример. Для решения квадратных неравенств используют метод интервалов.
Квадра́тное уравне́ние ![]()
(ср.р., р.п. квадратного уравнения)
Уравнение вида ax2 + bx + с = 0 (a ≠ 0). Виды квадратных уравнений – полное, неполное, приведённое. ![]()
Пример. Какие способы решения квадратного уравнения вы знаете?
Квадра́тные ско́бки ![]()
(мн., р.п. квадратных скобок)
Знаки [ ]. Используются для записи замкнутых промежутков, определения порядка действия в выражениях. ![]()
Пример. x ![]() [1, 10].
[1, 10].
Коллинеа́рные ве́кторы ![]()
![]()
(мн., р.п. коллинеарных векторов)
Векторы, которые лежат на одной прямой или на параллельных прямых. ![]()
Пример. Коллинеарные векторы либо одинаково направлены, либо противоположно направлены.
Коммутати́вный зако́н сложе́ния ![]()
(м.р., р.п. коммутативного закона сложения)
От перестановки слагаемых сумма не изменяется. То есть для любых двух натуральных чисел a и b верно равенство: a + b = b + a. ![]()
Пример. Коммутативный закон сложения используют, чтобы упростить вычисления.
Коммутати́вный зако́н умноже́ния ![]()
(м.р., р.п. коммутативного закона умножения)
От перестановки множителей произведение не изменяется. То есть для любых натуральных чисел a и b верно равенство: ab = ba. ![]()
Пример. Коммутативный закон умножения используют, чтобы упростить вычисления.
Компле́ксное число́ ![]()
(ср.р., р.п. комплексного числа)
Сумма вида a + bi, где a и b – действительные числа, а число i – мнимая единица, i2 = –1. ![]()
Пример. Числа 4 + 5i, –2 + 7i, 25 – 9i – это комплексные числа.
Компоне́нта ![]()
(сущ., ж.р., р.п. компоненты)
1. Составная часть, элемент чего-либо. ![]()
2. Один из элементов, совокупность которых определяет данный математический объект. ![]()
Пример. Компоненты действия сложения – это слагаемые.
Коне́чная десяти́чная дробь ![]()
(ж.р., р.п. конечной десятичной дроби)
Дробь, у которой после запятой стоит конечное число цифр. ![]()
Пример. Числа 3,1; 4,65; –9,0102 – это конечные десятичные дроби.
Коне́чное мно́жество ![]()
(ср.р., р.п. конечного множества)
Множество, состоящее из конечного числа элементов. ![]()
Пример. Множество цифр {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} – это конечное множество.
Конста́нта ![]()
(сущ., ж.р., р.п. константы)
То же, что Постоянная величина ![]()
Координа́та ![]()
![]()
![]()
(сущ., ж.р., р.п. координаты)
1. Точка координатной оси, которой соответствует действительное число. ![]()
2. Одно из чисел, совокупность которых характеризует положение точки; каждая координата имеет свой порядковый номер. ![]()
Пример. На плоскости точка имеет две координаты – абсциссу и ординату, в пространстве – три координаты – абсциссу, ординату и аппликату.
прил. координатный, -ая, -ое, -ые
Координа́тная ось ![]()
![]()
(сущ., м.р., р.п. номера)
Прямая, которая служит для изображения действительных чисел и на которой заданы положительное направление, начало отсчёта и единица длины. ![]()
Пример. Система координат на плоскости состоит из двух координатных осей, которые пересекаются в начале отсчёта.
Координа́тная пло́скость ![]()
![]()
(ж.р., р.п. координатной плоскости)
Плоскость, на которой задана система координат. ![]()
Пример. На координатной плоскости отметьте точку A(–3; 6).
Координа́тный луч ![]()
(м.р., р.п. координатного луча)
Одна из частей, которая получена в результате деления координатной оси начальной точкой (началом отсчёта). ![]()
Пример. Начало отсчёта точка О делит координатную ось на два координатных луча.
Координа́тный у́гол (квадра́нт) ![]()
![]()
(м.р., р.п. координатного угла)
Одна из четырёх частей координатной плоскости между двумя перпендикулярными координатными осями. ![]()
Пример. У точки, которая лежит в первом координатном углу, все координаты – положительные числа.
Ко́рень ![]()
(сущ., м.р., р.п. ко́рня)
1. Результат операции извлечения корня. Виды: корень квадратный, корень кубический, корень степени n и другие. ![]()
2. Решение уравнения. ![]()
3. Число, которое после подстановки вместо переменной обращает многочлен в нуль. ![]()
Пример. 1. Извлеките корень пятой степени из числа 32.
2. Запишите формулу корней квадратного уравнения.
3. Найдите корни многочлена x3 + 3x2 + 3x + 1.
Ко́рень уравне́ния ![]()
(м.р., р.п. корня уравнения)
Численное значение неизвестного, которое обращает данное уравнение в тождество (верное числовое равенство). ![]()
Пример. Найдите корни квадратного уравнения 2x2 + 7x – 9 = 0.
Ко́синус ![]()
(сущ., м.р., р.п. косинуса)
1. Тригонометрическая функция y = cos x. ![]()
2. Абсцисса конца подвижного единичного радиус-вектора. ![]()
Пример. Найдите cos 45°.
Косинусо́ида ![]()
![]()
(сущ., ж.р., р.п. косинусоиды)
Кривая линия, график функции y = cos x. ![]()
Пример. Изобразите на чертеже косинусоиду.
Кота́нгенс ![]()
![]()
(сущ., м.р., р.п. котангенса)
1. Тригонометрическая функция y = ctg x. ![]()
2. Отношение абсциссы конца подвижного единичного радиус-вектора к его ординате. ![]()
Пример. Найдите ctg 60°.
Коэффицие́нт ![]()
(сущ., м.р., р.п. коэффициента)
Числовой множитель при буквенном выражении, известный множитель при неизвестном выражении, постоянный множитель при переменной величине. ![]()
Пример. Назовите коэффициенты квадратного уравнения 5x2 + 12x – 8 = 0.
Кра́йний член ![]()
(м.р., р.п. крайнего члена)
Величины а и d в пропорции а : b = c : d. ![]()
Пример. Назовите крайние члены пропорции 15 : 45 = 23 : x.
Кра́тное натура́льного числа́ a ![]()
(ср.р., р.п. кратного натурального числа a)
Натуральное число b, которое делится нацело (без остатка) на число a. ![]()
Пример. Десять – это кратное числа 2.
Крива́я ли́ния ![]()
![]()
(ж.р., р.п. кривой линии)
Линия с неодинаковым направлением в каждой точке. ![]()
Пример. Парабола – это кривая линия второго порядка.
Кру́глые ско́бки ![]()
(мн., р.п. круглых скобок)
Знаки ( ). Используются для записи открытых промежутков, аргумента функции, указания порядка действий в выражении. ![]()
Пример. x ![]() (0; +∞
(0; +∞![]() ).
).
Л
Ле́вая часть ![]()
(ж.р., р.п. левой части)
Выражение, которое стоит слева от знака сравнения (=, ≠, >, <, ≥, ≤). ![]()
Пример. Левая часть равенства стоит слева от знака равно.
Лине́йное уравне́ние ![]()
(ср.р., р.п. линейного уравнения)
Уравнение, которое содержит неизвестные только в первой степени. ![]()
Пример. ax + b = 0 – линейное уравнение с одним неизвестным.
Ли́ния ![]()
![]()
(сущ., ж.р., р.п. линии)
1. Множество точек плоскости, координаты которых удовлетворяют уравнению
F(x, y) = 0. ![]()
2. Граница поверхности, которая имеет только одно измерение – длину. ![]()
Виды: прямая, кривая, ломаная. ![]()
Пример. Постройте на чертеже прямую линию.
прил. линейный, -ая, -ое, -ые.
Логари́фм ![]()
(сущ., м.р., р.п. логарифма)
Логарифмом числа b по основанию a называется показатель степени x, в которую надо возвести основание a, чтобы получить число b, то есть из равенства ax = b следует равенство x = loga b и наоборот. Также используют: натуральный логарифм loge b = ln b, десятичный логарифм log10 b = lg b. ![]()
Пример. Чему равен логарифм числа 1024 по основанию 2?
прил. логарифмический, -ая, -ое, -ие.
Логарифми́рование ![]()
(сущ., ср.р., р.п. логарифмирования)
Преобразование, при котором логарифм выражения с переменными приводится к сумме или разности логарифмов переменных. ![]()
Пример. Какое преобразование называется логарифмированием?
гл. логарифмировать, прологарифмировать
Логарифми́ческая фу́нкция ![]()
![]()
![]()
![]()
(ж.р., р.п. логарифмической функции)
Одна из основных элементарных функций y = loga x (a > 0, a ≠ 1), обратная показательной функции y = ax (a > 0, a ≠ 1). ![]()
Пример. Опишите свойства и постройте график логарифмической функции y = log2 x.
Логарифми́ческое выраже́ние ![]()
(ср.р., р.п. логарифмического выражения)
Выражение, которое содержит переменную под знаком логарифма. ![]()
Пример. Приведите пример логарифмического выражения.
Логарифми́ческое нера́венство ![]()
(ср.р., р.п. логарифмического неравенства)
Неравенство, которое содержит переменную под знаком логарифма. ![]()
Пример. Решите логарифмическое неравенство ![]() .
.
Логарифми́ческое уравне́ние ![]()
(ср.р., р.п. логарифмического уравнения)
Уравнение, в котором неизвестное находится под знаком логарифма. Простейшее логарифмическое уравнение имеет вид loga x = b. ![]()
Пример. Назовите методы решения логарифмических уравнений.
Ло́маная ли́ния ![]()
![]()
(ж.р., р.п. ломаной линии)
1. Линия, у которой смежные отрезки (звенья) не лежат на одной прямой. ![]()
2. Фигура, которая состоит из последовательности точек и соединяющих их отрезков, причём смежные отрезки (звенья) не лежат на одной прямой. ![]()
Пример. Сколько звеньев содержит данная ломаная линия?
Луч (полупряма́я) ![]()
![]()
1. Часть прямой, которая имеет начало, но не имеет конца. ![]()
2. Часть прямой, которая расположена по одну сторону от какой-либо точки этой прямой и включает эту точку. ![]()
Пример. Точка делит прямую на два луча.