Разложение функций в ряды
Часто бывает необходимо представить функцию в простом и единообразном виде. Рассмотрим представление функции в виде степенного многочлена в окрестности некоторой точки ![]() на оси абсцисс. Такое разложение называют разложением в ряд Тейлора. Если разложение выполняется относительно точки x = 0 , то такое разложение называют разложением в ряд Маклорена.
на оси абсцисс. Такое разложение называют разложением в ряд Тейлора. Если разложение выполняется относительно точки x = 0 , то такое разложение называют разложением в ряд Маклорена.
Разложим функцию ![]() в степенной ряд в окрестности x = 1, т.е. в ряд Тейлора.
в степенной ряд в окрестности x = 1, т.е. в ряд Тейлора.
| > | restart:
series(exp(x),x=1); |
Рассмотрим еще один пример.
| > | series(exp(x),x); |
В последнем примере значение точки разложения неуказанно. В таком случае Maple раскладывает функцию точке x = 0, т.е. в ряд Маклорена. Число членов ряда может быть изменено третьим необязательным параметром – неотрицательным целым числом (по умолчанию оно равно 5) или системной переменной Order.
Ряд можно преобразовать в полином (исключить остаточный член) используя convert с параметром polynom.
Следующий пример демонстрирует разложение функции в ряд Маклорена с числом членов ряда от 1 до 40.
| > | restart:
with(plots): f:=x->sin(x)^2+cos(x); for i from 1 to 40 do Ris[i]:=plot([f(x),convert(series(f(x),x,i),polynom)],x=-8..8,y=-1..2,title=cat("Число членов ряда =", i)): end do: display([seq(Ris[i],i=1..40)], insequence=true); |
 |
В этом примере изображения, созданные функцией plot, записываются в одномерный массив Ris, а функция display с параметром insequence=true отображает изображения друг за другом, создавая анимированное изображение.
Для периодических функций часто используют разложение в тригонометрический ряд Фурье.
Такое разложение используют, например, для анализа сигналов электрических цепей. В Maple нет стандартной функции для такого разложения, поэтому покажем, как это можно сделать.
Тригонометрический ряд Фурье – это представление произвольной периодической функции f ( x) с периодом [-π, π] в виде
![]()
![]() где
где ![]()
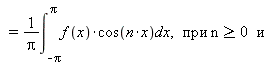
![b[n] = `/`(`*`(int(`*`(f, `*`(x, `*`(sin(`*`(n, `*`(x)))))), x = `+`(`-`(Pi)) .. Pi)), `*`(Pi)), `>=`(`*`(?@8, `*`(n)), 1.)](images/Maple_511.gif)
Числа ![]() и
и ![]() – называются коэффициентами Фурье функции f ( x) .
– называются коэффициентами Фурье функции f ( x) .
Рассмотрим пример разложения функции в тригонометрический ряд Фурье. Периодическая функция с периодам 2π определена следующим образом:
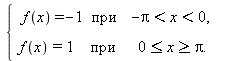
| > | restart:
a:=n->1/Pi*int(f(x)*cos(n*x),x=-Pi..Pi); b:=n->1/Pi*int(f(x)*sin(n*x),x=-Pi..Pi); FS:=(x,k)->a(0)/2+sum(a(n)*cos(n*x)+b(n)*sin(n*x),n=1..k); f:=x->piecewise(x>-Pi and x<0, -1,x>=0 and x <=Pi, 1); FS(x,15); |
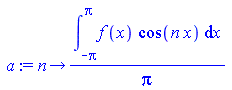 |
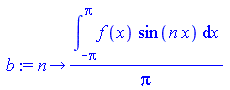 |
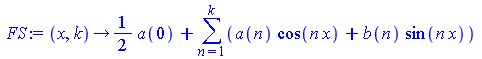 |
Выше представлено разложение функции f ( x) в тригонометрический ряд Фурье.
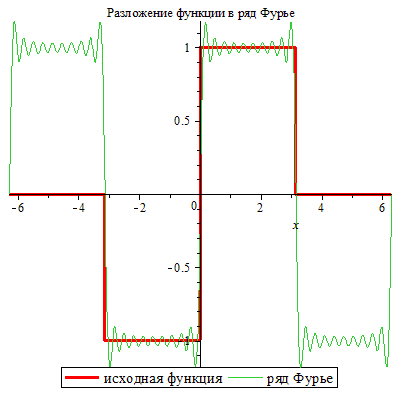
Изобразим исходную функцию и ее разложение.
| > | plot([f(x),FS(x,20)],x=-2*Pi..2*Pi,thickness=[3,1],legend=["исходная функция","ряд Фурье"],title="Разложение функции в ряд Фурье"); |
 |
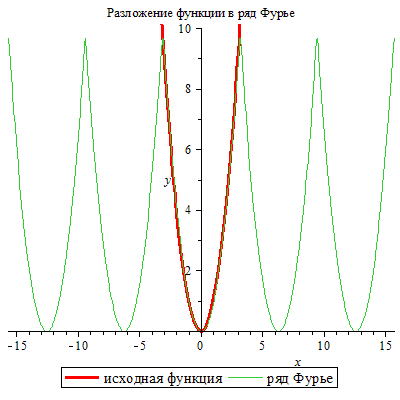
Рассмотрим еще один пример. Периодическая функция с периодам 2π определена следующим образом: ![]() .
.
| > | f:=x->x^2;
FS(x,15); |
Изобразим исходную функцию и ее разложение.
| > | plot([f(x),FS(x,20)],x=-5*Pi..5*Pi,y=0..10,thickness=[3,1],legend=["исходная функция","ряд Фурье"],title="Разложение функции в ряд Фурье"); |
 |