Кусочная функция 

Для задания кусочной функции в Maple имеется специальное средство – функция piecewise, которая имеет следующие параметры: piecewise (интервал_1, выражение_1, интервал_2, выражение_2, ..., интервал_n, выражение_n [,  выражение]).
Последнее необязательное выражение задает функцию для неохваченных интервалов. 

>	restart: p:=x-> piecewise(x<0,-x,x>0,x); plot(p(x),x=-1..1,scaling=constrained,title="Кусочная функция");

 

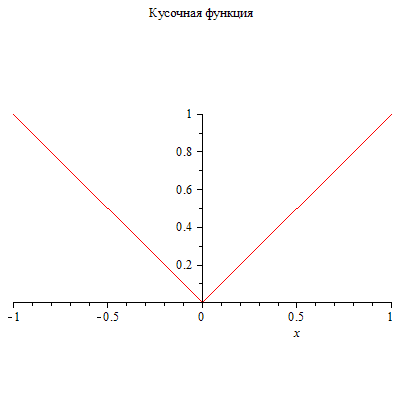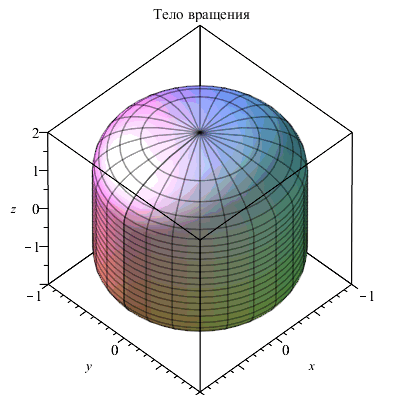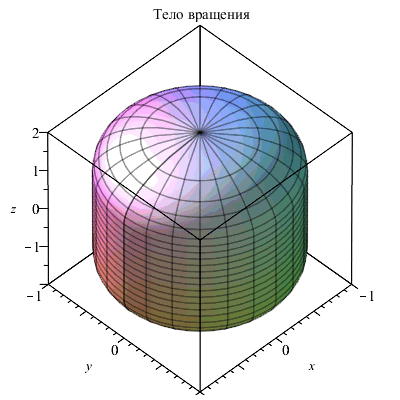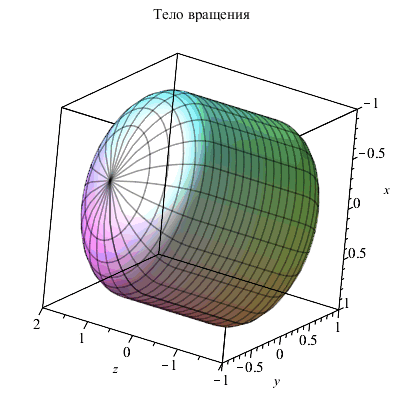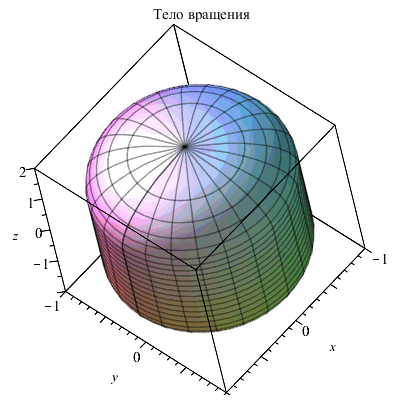
Кусочные функции интегрируются и дифференцируются теми же средствами, что и обычные функции. В следующем примере для вычисления объема и площади поверхности тела, образованного вращением вокруг оси z кусочной функции f ( z), использовались известные выражения: 

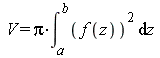
и 

>

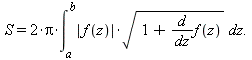
f := z-> piecewise( z>-2 and z<-1,sqrt(1-(z+1)^2),z>=-1 and z<=1,1,z>1 and z <2,sqrt(1-(z-1)^2)); plot(f(z),z=-2..2,scaling=constrained,title="Образующая"); plots[cylinderplot](f(z),theta=0..2*Pi,z=-2..2,axes=box,title="Тело вращения"); V:=Pi*int(f(z)^2,z=-2..2); S:=2*Pi*int(abs(f(z))*sqrt(1+diff(f(z),z)^2),z=-2..2);
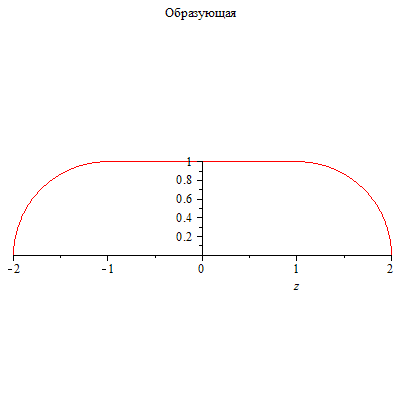