Аналитическое решение 

Для аналитического решения линейных и нелинейных уравнений и систем служит функция solve, например: 

>	solve(a*x^2+b*x+c=0,x);

 

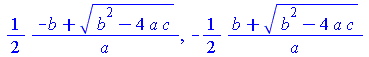В качестве первого параметра функции solve записано уравнение, а второго – переменная, относительно которой уравнение следует решать. Если правая часть уравнения равна нулю, то знак равенства и нуль могут быть опущены. 

Если найдено несколько решений уравнения, то корни записываются в виде последовательности. 

Аналогично может быть получено решение для неравенства. 

>	solve(x^2+x>5,x);

 

Open – открытый диапазон, т.е. указанное в скобках значение в него не входит. 

Если в качестве первого параметра функции solve будет множество, состоящее из уравнений, то Maple будет рассматривать это множество как систему. 

Решим систему линейных уравнений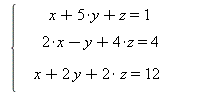  

>	solve({x+5*y+z=1,2*x-y+4*z=4,x+2*y+2*z=12},{x,y,z});

 

Рассмотрим еще один пример. Решим систему нелинейных уравнений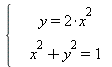  

Предварительно проиллюстрируем решение графически. 

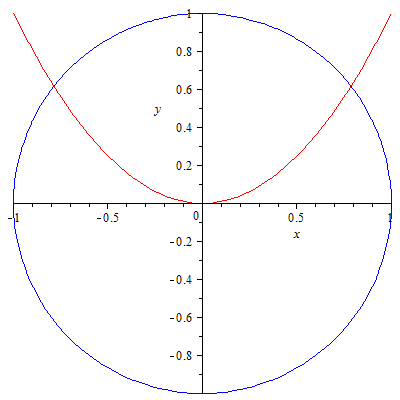
>	plots[implicitplot]([y=x^2,x^2+y^2=1],x=-1..1,y=-1..1,color=[red,blue]); solve({y=x^2,x^2+y^2=1},{x,y});

 

В решении присутствует выражение RootOf, означающее, что решение получено в неявной форме. Для вычисления решения в явной форме следует воспользоваться функцией allvalues. 

>	allvalues(%);

 

Преобразуем полученное решение к виду с плавающей точкой. 

>

evalf(%);

 

Система имеет два действительных корня (их видно на графике) и два комплексных. 

Функция solve, примененная для решения тригонометрического уравнения, выдает только главные решения, то есть решения в интервале [0, 2π ]. Для того, чтобы получить все решения, следует указать параметр allsolutions. 

>	solve(5*sin(x)+12*cos(x)=5,x); solve(5*sin(x)+12*cos(x)=5,x, allsolutions);