Все реальные объекты отображаются на картах какими либо условными знаками, точками, линиями, полигонами или поверхностями. Кроме того, немаловажным фактором является цветовая градация объектов, например изображение ландшафта или распределение плотности населения. Примеры картографического представления объектов реального мира основными типами графических примитивов можно увидеть на рис. 2.1.

Рис. 2.1. Объекты реального мира и картографическое представление

        Точки, линии, области и поверхности вместе могут представлять большинство природных и социальных феноменов, которые мы встречаем каждый день. В рамках ГИС объекты реального мира явно представляются тремя типами объектов из указанных. Точки, линии и области могут представляться соответствующими символами, поверхности же представляются чаще всего либо высотами точек, либо другими компьютерными средствами. Феномены непространственные по своей природе не могут непосредственно исследоваться в ГИС, если только им не присвоить некоторые представляющие их пространственные характеристики. Рассмотрим пространственные объекты более подробно.

        Точечные объекты - это такие объекты, каждый из которых расположен только в одной точке пространства. Примером таких объектов могут быть деревья, дома, перекрестки дорог, и многие другие. О таких объектах говорят, что они дискретные, в том смысле, что каждый из них может занимать в любой момент времени только определенную точку пространства. В целях моделирования считают, что у таких объектов нет пространственной протяженности, длины или ширины, но каждый из них может быть обозначен координатами своего местоположения. В действительности, все точечные объекты имеют некоторую пространственную протяженность, пусть самую малую, иначе мы просто не смогли бы их увидеть. Принимаем отсутствие длины и ширины так, что, например, при измерениях атмосферного давления, характеризуемых потенциально бесконечным числом точек, сами точки всегда занимают определенные местоположения без каких-либо перекрытий. Масштаб, при котором мы наблюдаем эти объекты, задает рамки, определяющие представление этих объектов как точек. Например, если вы смотрите на дом с расстояния нескольких метров, то сооружение выглядит внушительным и имеет существенные длину и ширину. Но это представление меняется, когда вы начинаете отдаляться: чем дальше, - тем меньше дом выглядит как площадный объект, тем больше — как точечный.

        Линейные объекты представляются как одномерные в нашем координатном пространстве. Такими "одномерными" объектами могут быть дороги, реки, границы, изгороди, любые другие объекты, у которых один из геометрических параметров существенно больше другого. Масштаб, при котором мы наблюдаем эти объекты, опять же, обусловливает порог, при пересечении которого мы можем считать эти объекты не имеющими ширины. Как вы знаете, реки, дороги, изгороди имеют два измерения при близком рассмотрении. Но чем дальше мы от них, тем более тонкими они становятся. Постепенно они становятся такими тонкими, что оказывается возможным представить их себе как линейные объекты. Другие линии, такие как политические границы, вообще не имеют ширины. В действительности, эти линии даже не являются материальными сущностями, а возникают как следствие политических соглашений.

        Для линейных объектов, в отличие от точечных, мы можем указать пространственный размер простым определением их длины. Кроме того, поскольку они не занимают единственное местоположение в пространстве, мы должны знать, по меньшей мере, две точки - начальную и конечную - для описания местоположения линейного объекта в пространстве. Чем сложнее линия, тем больше точек нам потребуется для указания точного ее расположения. Опираясь на геометрию, мы можем также определять формы и ориентации линейных объектов.

        Объекты, рассматриваемые с достаточно близкого расстояния, чтобы иметь и длину и ширину, называются областями или площадными объектами. Примеры областей, или "двухмерных" объектов, включают территории, занимаемые двором, городом или целым континентом. При определении местоположения области в пространстве мы обнаруживаем, что ее граница является линией, которая начинается и кончается в одной и той же точке. Помимо указания местоположения областей через использование линий, мы можем себе представить теперь три характеристики: как и для линий, мы можем указывать их форму и ориентацию, а теперь еще и величину площади, которую область занимает.

        Добавление нового измерения, высоты, к площадным объектам позволяет нам наблюдать и фиксировать поверхности. Хотя мы можем рассматривать дом с близкого расстояния и описывать его в терминах его общей длины и ширины, нам часто нужно знать, сколько в нем этажей. В таком случае нам нужно рассматривать дом не как плоскую область, а как трехмерный объект, имеющий длину, ширину и высоту. Поверхности окружают нас повсюду. Холмы, долины, гряды гор, скалы и множество других образований могут описываться указанием их местоположения, занимаемой площади, ориентации, и теперь, с добавлением третьего измерения, их высот [3].

        Поверхности состоят из бесконечного числа точек со значениями высот. Мы говорим, что они непрерывны, поскольку эти точки распределены без разрывов по всей поверхности, что показано на рис. 2.2. В действительности, поскольку высота трехмерного объекта меняется от точки к точке, мы можем также измерять величину изменения высоты с перемещением от одного края до другого. Имея такую информацию, мы можем определить объем материала в выбранном образовании. Возможность таких вычислений весьма полезна, когда нам нужно узнать, сколько воды содержится в водоёме или сколько материала (пустой породы) лежит поверх угольного пласта.

                               

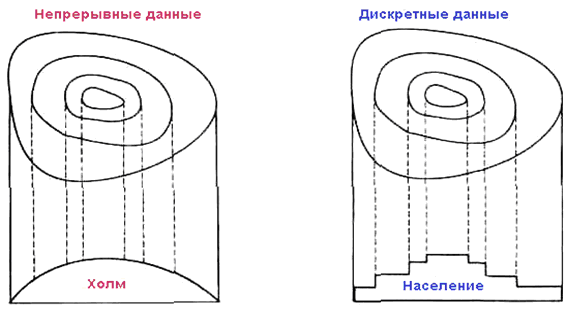
                                                Рис. 2.2. Непрерывные и дискретные поверхности